rumpek: To teraz jakiś taki trochę naciągany dowód, lecz teoretycznie poprawny.
Zacznijmy wpierw od założeń (najważniejsze):
α, β, γ, ∡CSB > 0
Oznaczyłem sobie |∡A| = 2γ oraz |∡B| = 2α i |∡C| = 2β
skoro mamy podane, że dwusieczne kątów, więc dzielą te kąty na pół dlatego mamy β i α.
Zajmijmy się samym trójkątem ABC (sumą kątów):
180
o = 2α + 2β + 2γ / :2
90
o = α + β + γ
 α + β = 90o − γ
α + β = 90o − γ 
Teraz rozpatrzmy trójkąt CSB:
180
o = α + β + ∡CSB
Podstawiamy teraz równanie z pierwszego podpunktu:
180
o = 90
o − γ + ∡CSB
180
o − 90
o + γ = ∡CSB
∡CSB = 90o + γ
Jako iż wiemy, że kąt γ jest większy od zera (inaczej trójkąt by nie istniał) oraz wiemy, że
kąt rozwarty jest wtedy gdy jest większy od 90
o. Zatem kąt ∡CSB jest większy od 90
o.
c.n.u.
(niech sprawdzi to jakiś "koksu" z dowodów

bo to nie jest mój dział )

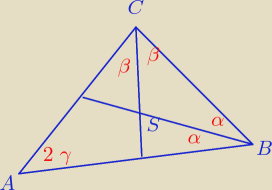 Wpierw rysunek, bo ten edytor teraz jakoś strasznie wolno działa, aż się rysować nie chce.
Wpierw rysunek, bo ten edytor teraz jakoś strasznie wolno działa, aż się rysować nie chce.
 α + β = 90o − γ
α + β = 90o − γ  Teraz rozpatrzmy trójkąt CSB:
180o = α + β + ∡CSB
Podstawiamy teraz równanie z pierwszego podpunktu:
180o = 90o − γ + ∡CSB
180o − 90o + γ = ∡CSB
∡CSB = 90o + γ
Jako iż wiemy, że kąt γ jest większy od zera (inaczej trójkąt by nie istniał) oraz wiemy, że
kąt rozwarty jest wtedy gdy jest większy od 90o. Zatem kąt ∡CSB jest większy od 90o.
c.n.u.
(niech sprawdzi to jakiś "koksu" z dowodów
Teraz rozpatrzmy trójkąt CSB:
180o = α + β + ∡CSB
Podstawiamy teraz równanie z pierwszego podpunktu:
180o = 90o − γ + ∡CSB
180o − 90o + γ = ∡CSB
∡CSB = 90o + γ
Jako iż wiemy, że kąt γ jest większy od zera (inaczej trójkąt by nie istniał) oraz wiemy, że
kąt rozwarty jest wtedy gdy jest większy od 90o. Zatem kąt ∡CSB jest większy od 90o.
c.n.u.
(niech sprawdzi to jakiś "koksu" z dowodów  bo to nie jest mój dział )
bo to nie jest mój dział )