funkcja kwadratowa
helpp: wykres funkcji y= |x−2| przecina okrąg o: x2 + y2 −4x−4=0 w punktach A i B. a) oblicz
współrzędne punktów A i B b) wykaż ze trójkąt ABS, gdzie S jest środkiem okręgu o, jest
prostokątny. c) oblicz pole figury F= F1 n ( część wspólna) F2 , jesli F1 = {(x,y): x ∊ R i x2
+ y2 − 4x − 4 ≤0}, f2={(x,y): x ∊ R i y ∊ R i y≤ | x− 2|}
12 gru 19:14
helpp: czy doprze rozumiem w punkcie a należy przyrównać wzory funkcji?
12 gru 19:22
krystek:
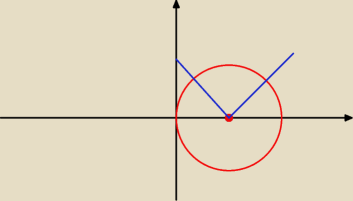
12 gru 19:31
krystek: układ r−ń
dlax≥2 masz y=x−2 i okrąg
Dla x,<2 masz y=−x+2 i okrąg. wyznaczasz A iB
12 gru 19:33
helpp: dzięki za rys, a jak mam wykazać punkt b
12 gru 19:34
krystek: Oblicz IABI i z Pitagorasa!
12 gru 19:48
helpp: myślę że cięciwę łączącą punkty A i B można obliczyć z długości wektora AB, potem odcinki AS i
BS są promieniami okręgu i są sobie równe, czy mogę zastosować twierdzenie odwrotne do tw
Pitagorasa
12 gru 19:50
