stereometria załamany :(: łącząc ze sobą środki ciężkosci sasiednich scian czworoscianu foremnego o krawedzi długosci a otrzymamy czworoscian o jakiej krawedzi ? potrzebuje jakiegos pomysłu na to zadanko i jestem otwarty na propozycje rozwiazania.

załamany :(: up

Andrzej: tak na szybko: Czworościan ABCD AE − wysokość (i jednocześnie środkowa) trójkąta ABC DE − to samo w trójkącie BCD E jest środkiem krawędzi BC znajdź cosinus kąta AED szukaną krawędź wylicz teraz z twierdzenia cosinusów.

Andrzej: a teraz tak na wolniej chyba niepotrzebne nawet te cosinusy wystarczy zwykłe podobieństwo trójkątów P − środek ciężkości ABC, Q − środek ciężkości BCD trójkąt AED jest podobny do PEQ w skali 3 : 1

załamany :(: hmm dzieki na wolno musze to przekminic

krystek: Narysuj przekrój łącząc wierzchołek tego czworościanu ze środkami dwóch krawędzi podstawy i zauważ skale podobieństwa jaka jest( takie jest moje spostrzeżenie)

załamany :(: kminie narazie z tw cos bo to lepiej rozumie niz podobienstwo

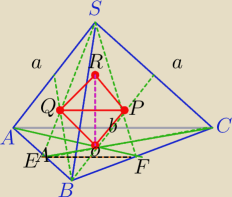
Mila: 1) Punkty O, P,Q,R dzielą wysokości ścian w stosunku 2:1 2)

	1
W ΔAFS: |OF|≡|PF|=		h
	3

|AF|=h, |OP|=b

OF		h		(1/3)h		h		1
	=		⇔		=		⇔b=
OP		a		b		a		3

analogicznie z pozostałymi odcinkami : OQ, QR,PR,

	SP		h		(2/3)h		h
Albo inaczej:		=		⇔		=
	PQ		EF		PQ		1   a 2

	1
|PQ|=		a}
	3

	1
Krawędź b szukanego czworościanu PQRO jest równa		a.
	3