zadanie
tn: czy równanie kwadratowe może mieć nieskończenie rozwiązań?
11 gru 16:50
l: tak
11 gru 16:51
ICSP: równanie kwadratowe jest stopnia II
Twierdzenie:
"Każdy wielomian stopnia n−tego posiada n pierwiastków"
odpowiedz sobie teraz sam na swoje pytanie.
11 gru 16:52
Basia:
ICSP to twierdzenie nie jest prawdziwe
Ono brzmi tak:
Wielomian n−tego stopnia ma nie więcej niż n pierwiastków rzeczywistych.
11 gru 16:55
pszczółka Maja:
Twierdzenie podane przez ICSP nie jest prawdziwe w R
11 gru 16:55
Basia:
no może być też ma co najwyżej ........
11 gru 16:56
Aga: Każdy wielomian stopnia n−tego w R posiada co najwyżej n pierwiastków.,
a w liczbach zespolonych n pierwiastków.
11 gru 16:56
ICSP: ja już uznaje liczby zespolone więc jest prawdziwe
11 gru 16:57
Basia:
ICSP mieszasz w ten sposób dzieciakom w łepetynach.
I dobrze o tym wiesz łobuzie.
11 gru 17:03
ICSP: oj tam oj tam
11 gru 17:09
tn: w końcu jak jest
?
11 gru 17:10
tn: już wiem, nie może mieć. dziękuję Basia za POPRAWNE przytoczenie twierdzenia
11 gru 17:11
tn: maxymalnie dwa, tak samo wielomian trzeciego stopnia maxymalnie 3
11 gru 17:12
Aga: Pyta licealista, czy student?
11 gru 17:12
tn: licealista a co?
11 gru 17:13
Trivial:
Zasadnicze twierdzenie algebry mówi o tym, że w liczbach zespolonych każdy wielomian stopnia n
ma dokładnie n pierwiastków (zespolonych lub nie) z uwzględnieniem krotności.
Dla liczb rzeczywistych mamy:
Każdy wielomian stopnia n ma co najwyżej n pierwiastków rzeczywistych.
11 gru 17:13
tn: no taka odpowiedź jest jasna
11 gru 17:14
tn: Trivial jest od Ciebie jakiś kontakt przez gg
11 gru 17:15
Trivial: Jest, ale tylko ludzi, których znam w realu.
11 gru 17:15
tn: aha, szkoda chciałem omówić z Tobą pewno zadanie algorytmiczne, na forum ciężko, ale nic
11 gru 17:16
Trivial: możesz pisać na forum, akurat nic nie mam do roboty.
11 gru 17:20
tn: na forum jest niewygodnie, ale niech będzie
11 gru 17:28
tn: opisze zadanko pokrótce
11 gru 17:28
tn: wyobraźmy sobie układ współrzędnych( a może graf)
11 gru 17:29
tn: jest to I ćwiartka (dodatnie współrzędne). Dostajemy n współrzędnych powiedzmy dla przykładu n
=5
Potem dostaniemy parę dwóch współrzędnych. Teraz naszym zadaniem jest wypisanie. Do którego
punktu 1 czy drugiego mają bliżej wspólrzedne podane na początku
11 gru 17:31
tn: najbliższa droga to droga po krawędziach układu współzędnych nie po przekątnej
11 gru 17:32
tn: np:
4 współrzędnych na początek( jest ograniczenie współrzędnych podane :
np. (5 na 6)
1,2
3,4
5,6
2,3
oraz dwie kolejne:
1)0,0 ;2)2, 1
teraz tak:
11 gru 17:34
tn: mamy znaleźć ile spośród tych czterech punktów ma najbliżej do
1 lub 2
jeśli np. 3 współrzędne mają do drugiego to piszemy: 3
i mamy sprawdzić ile ma najbliżej do 1 założmy jeden,
mamy sprawdzić ile równo do obu założmy 0 piszemy zero
11 gru 17:36
tn: więc mniej wiecej na tym polega zadanie
11 gru 17:37
tn: (jeszcze jedna nieścisłość)
równanie stopnia pierwszego moze mieć przecież nieskończenie rozwiązań
11 gru 17:37
Trivial: Podaj przykład takiego równania
11 gru 17:38
tn: 5x = 5x
11 gru 17:39
tn: przecież ile razy robiłem zadanie z funkcji liniowej wyznacz dla jakich parametrów m równanie
ma nieskończenie wiele rozwiązan
11 gru 17:40
Trivial: Chodziło o wielomian stopnia n. Wielomian stopnia n nie może mieć zera przy x
n.
11 gru 17:43
tn: to jak z tymi zadaniami, przecież robiłem takie zadania z parametrami
11 gru 17:44
Trivial: Jak ci się wszystko poskraca, to wiadomo, że może mieć nieskończoną ilość rozwiązań.
11 gru 17:45
tn: czyli może mieć?
11 gru 17:46
Trivial:
Co do problemu to możemy sprawdzić po kolei jaka jest droga każdego punktu od punktu 1 i 2.
Powiedzmy, że chcemy sprawdzić drogę s punktu P = (x,y) od punktu A = (a, b). Droga ta wynosi:
s(P, A) = |x−a| + |y−b|.
Wyniki zapisujemy w dwuwymiarowej tablicy s[n][m], gdzie n oznacza ilość punktów, a m ilość
punktów, do których drogę będziemy sprawdzać. Potem znaleźć minimum i policzyć ile wystąpień
tego minimum było i koniec.
11 gru 17:47
Trivial: Jeżeli chodzi ci o równanie typu:
x2 + 2 = x2 + 2
To może.
11 gru 17:48
tn: czyli tożsamościowe ?
Trivial, tak właśnie robię z tymi modulami.
Ale takie rozwiązanie jest o wiele za powolne
11 gru 17:49
Trivial:
Takie rozwiązanie nie jest powolne. Zabiera tylko O(nm) czasu. Da się jakoś szybciej w ogóle?
11 gru 17:51
tn: właśnie dlatego mam problem, jest zbyt powolne:
bo nie powiedziałem, ale może zdarzyć się że będzie par dwóch punktów 100 000 podanych przez
usera, lecz mapa się nie zmieni
11 gru 17:56
tn: w sensie user może podać 100 000 takich par punktów i dla wszystkich trzeba sprawdzić
11 gru 17:56
Trivial:
Od kiedy czas wielomianowy jest powolny?
Można ograniczyć zużycie pamięci, ale czasu
obliczeniowego raczej już bardziej nie wyśrubujesz − skąd mamy wiedzieć, czy punkt który był
bardzo daleko od punktu A=(0,0) nie jest najbliżej punktu A=(100,100)? Musimy to sprawdzić.
11 gru 18:01
Trivial: Chyba, że znasz jakiś cudowny sposób na szybkie sprawdzanie, które punkty są odległe o daną
liczbę kroków (np. o 5) od danego punktu A − wtedy rzeczywiście można to usprawnić i nawet mam
pewien pomysł.
11 gru 18:05
Trivial: No więc? Jakieś pomysły?
11 gru 18:11
tn: ja nie mam na razie pomysłu.
uważam, że należy jakoś sporządzić drzewo lub inną strukturę danych, która dla danego opisu
mapy pomoże nam szybko ustalić ilość dalszych i bliższych
11 gru 18:17
tn: jakaś wskazówka?
11 gru 18:26
Trivial: Sam myślę nad rozwiązaniem. Mam pewne pomysły, ale wszystkie są wolniejsze albo takie same jak
O(nm). Nie wiem czy dobrze rozumiem, ale czy ilość punktów A może się zmieniać? (punkty A, to
te punkty, od których sprawdzamy ile jest punktów P leżących najbliżej).
11 gru 18:30
tn: są dwa punkty o współrzędnych podanych przez usera:x1, y1, x2,y2
(tych punktów będzie q− user wybiera ile konifguracji będzie sprawdzal)
Jedna user podaje n punktów oraz ich współrzędnez reguły będzie ich wiecej niż dwa
i one się nigdy nie zmienią
11 gru 18:37
Trivial: tych punktów będzie q?
11 gru 18:42
Trivial: Czy 2?
11 gru 18:42
Trivial:
"oraz ich współrzędnez reguły będzie ich wiecej niż dwa i one się nigdy nie zmienią"
Motasz panie. Można trochę jaśniej?
11 gru 18:45
tn: user powie tak jakby ile zestawów danych;
ale te zestawy danych to 2 współrzędnych, dla każdej mamy obliczyć wiadomo co
11 gru 18:46
Trivial:
Albo inaczej, powiedz czy dobrze rozumiem:
1. Wszystkie punkty mają po dwie współrzędne.
2. Mamy dwa punkty:
A = (xa, ya)
B = (xb, yb).
3. User podaje jeden miliard (albo n) punktów P:
P1 = (x1, y1)
P2 = (x2, y2)
...
Pn = (xn, yn)
4. Mamy sprawdzić które punkty P leżą najbliżej punktów A i B i je policzyć.
11 gru 18:48
tn: tak: dostajemy:
n punktów.
Potem dowiadujemy się, będę chciał sprawdzać dla np. 3 par:
wiec dostaniemy kolejno trzy pary punktów( pierwszy punkt w parze i drugi):
i naszym zadaniem jest sprawdzić ile spośród n punktów leży bliżej pierwszego, drugiego oraz w
równej odległości
11 gru 18:52
Trivial:
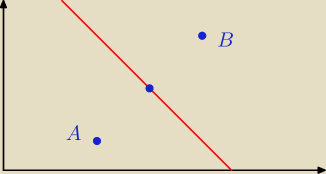
No to w takim razie wcześniej nie zrozumiałem chyba zadania.
Wyznaczamy prostą, która będzie równoodległa od punktów A i B.
1. Wszystkie punkty P, które leżą po stronie 'A' są bliżej punktu A.
2. Wszystkie punkty P, które leżą po stronie 'B' są bliżej punktu B.
3. Wszystkie punkty P, które leżą na prostej są równoodległe od A i B.
Czy o to chodziło?
11 gru 19:06
tn: ok, tak o to chodziło, przemyślę Twoje rozumowanie i spróbuję − wydaje sie, że mi pomogłes
11 gru 19:13