granice ciagu Wojtek: Korzystając z definicji granicy ciagu wykaż że:

	1
a) limn→∞
	n2

Jak zrobić ten przykład korzystając z tej definicji której nie potrafię zrozumieć. Czy da się zrobić ten przykład w inny sposób np. wyłączając czynnik przed nawias − tak robiliśmy na zajęciach ale treść zadania było oblicz granice.

Trivial: Nie ma czego wykazać.

Wojtek: a sorki wykazać że jest równe 0

Trivial: To się robi np. tak: lim_n→∞ a_n = g :⇔ ∀ε>0 ∃n₀∊ℕ : ∀n>n₀ |a_n − g| < ε.

	1
an =
	n2

g = 0 Czyli wychodząc ze strony prawej mamy:

	1
|		− 0| < ε
	n2

	1		1
|		| < ε //		zawsze > 0, moduł opuszczamy.
	n2		n2

1
	< ε
n2

εn² > 1

	1
n2 >
	ε

	1
n >
	√ε

	1
Wystarczy wybrać n0 := [		+ 1], wtedy ∀n>n0 |an − g| < ε czyli OK.
	√ε

Wojtek: nie rozumiem i tak tego nawet nie wiem co oznaczaja te znaki widzę i wiem jak obliczyłes n ale z kąd to się wzieło i n0 tez nie wiem jak zrobiles i w końcu nie wiem czy jest rowne 0

Trivial:

	1
n0 biorę liczbę naturalną o przynajmniej o jeden większą od		. Te znaczki oznaczają
	√ε

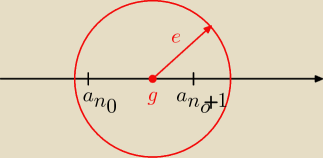
takie coś: Mamy pewien ciąg a_n. Określamy dokładność ε. Chcemy znaleźć takie n₀, aby dla wszystkich n większych od n₀ wyrazy ciągu a_n były oddalone od granicy g mniej niż ε. Jeżeli możemy to zrobić dla dowolnego ε, to g jest wtedy granicą ciągu a_n.

Wojtek: ok to ja spróbuję zrobic 2 przykład

	3n
b) limn>∞		=35
	5n+2

	3n
an=
	5n+2

g=³₅

	3n
|		−35|<e
	5n+2

	15n		45n
|		−		|<e
	25n+10		25n+10

	30n		30n
|−		|<e //−
	25n+10		25n+10

30n
	<e
25n+10

6n
	<e
5n+2

i nie wiem gubie sie dalej nie chce durnot wypisywac

Trivial:

	3n		3		5*3n		3(5n+2)		15n − (15n+6)
|		−		| = |		−		| = |		| =
	5n+2		5		5*(5n+2)		5(5n+2)		25n+10

	6		6
= |−		| =		.
	25n+10		25n+10

	6
		< ε
	25n+10

Wyznaczyć z tego n jako funkcję n(ε), a potem wziąć n₀ np. liczbę naturalną o jeden większą od tego n.

Wojtek: chyba odpuszczę sobie to zadanie, cięzko mi to idzie. Nie wiem jak wyznaczyć n jeśli e też jest moją niewiadomą

Trivial: ε nie jest niewiadomą. ε to parametr.

Trivial: 6 < ε(25n + 10) 6 < 25εn + 10ε 6−10ε < 25εn

	6−10ε
n >
	25ε

	6−10ε
Skoro n ma być większe od		to wystarczy wybrać jakąkolwiek liczbę naturalną
	25ε

	6−10ε
większą od		i mamy OK. Zauważ, że dla każdego ε istnieje taka liczba (nasze n0).
	25ε

np.:

	6−10ε
n0 = [		+ 1]
	25ε