f Stokrotka:

	π
Oblicz tg
	12

dasd: γ≤sdadasdasd

dasd: ∞ΩΩΩΩΩΩΩΔ

Stokrotka: dzieki

dasd: e to jest online

dasd: roziazac ci to

Stokrotka: tak

dasd: 4

dasd: Co bede z tego miał

Stokrotka: ładne podziekowanie .

dasd:

dasd: a moze lodzika

Aga:

1		1		1
	π=		π−		π
12		3		4

ze wzoru tg(x−y)

Stokrotka: pomozesz czy nie?

Stokrotka: okej sprobuje

Stokrotka:

	π
czyli to bedzie tg(U{π}[3} −		) ?
	4

Stokrotka: nie wiem jak to zrobic .. Aga pomozesz?

Aga: Napisz wzór na tg(x−y)

	π		π
za x podstaw		, za y napisz
	3		4

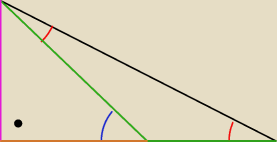
ICSP: ja pozwolę sobie pokazać inny sposób Oczywiście jeśli nikt się nie obrazi. Czerwone kąty mają po 15^o. Oczywiste jest więc zatem ze niebieski kąt ma 30^o. Z tego wynika że jeżeli różowy odcinek oznaczę jako x to : pomarańczowy = x√3 zielony = 2x

	różowy		x
tg15o =		=		= 2 − √3
	pomarańczowy + zielony		x(2 + √3)

Pozdrawiam

dasd:

Stokrotka: fajny sposob ale ja musze zrobic to ze wzorow?

Stokrotka: aga podstawiam ale nie wiem co dalej

ICSP: Jeżeli w poleceniu nie będzie nic napisane to nie mają się do czego przyczepić. Aga masz może link do tematu w którym tłumaczyłaś komuś metodę Chio? Mam dziś chwilkę czasu to mógłbym się z nią zaprzyjaźnić

ICSP: albo tak :

	√6 − √2
sin15o =
	4

	√6 + √2
cos15o =
	4

	sin15o		√6 − √2		4		√6 − √2)2
tg15o =		=		*		=		=
	cos15o		4		√6 + √2		4

	8 − 4√3
		= 2 − √3
	4

Aga:

	tgx−tgy
tg(x−y)=
	1+tgx*tgy

	1
x=		π
	3

	1
y=		π
	4

tgx=√3 tgy=1

	1		1		√3−1
tg(		π−		π)=		=2−√3
	3		4		1+√3

Aga: @ICSP , a po co się obrażać, im więcej pomysłów tym lepiej, każdy znajdzie coś dla siebie

Stokrotka: dzieki kochani ! jestescie wspaniali