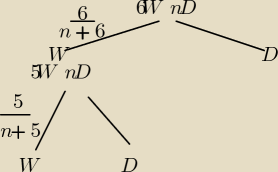
Obliczanie prawdopodobieństwa dla wartości n Bleek: W dostawie n kalkulatorów, 6 jest wadliwych. Dla jakich wartości n prawdopodobieństwo tego, że dwa zakupione kalkulatory są wadliwe jest mniejsze od ¹₃ Zrobiłem takie drzewko, jak narysowałem. (6W − ilość wadliwych, nD − ilość dobrych) Przyrównałem prawdopodobieństwo wylosowania dwóch wadliwych: (⁶_n+6)*(⁵_n+5)<¹₃ Po rozwiązaniu wychodzi wielomian kwadratowy: −n²−11n+60<0 i rozwiązaniem jego jest n∊(−∞;−16¹₂)u(5¹₂;+∞) wiadomo, że n musi być większe lub równe 1 więc zostaje tylko n>5¹₂ Sam fakt, że wychodzi ułamek jest dziwny, poza tym odpowiedź do zadania w książce brzmi n>10 Czy zadanie należy wykonać inaczej czy popełniłem jakiś błąd?

Gustlik: Najlepiej kombinatoryką:

	n 2		n!		(n−2)!*(n−1)*n		(n−1)n
|Ω|=		=		=		=
			2!(n−2)!		2(n−2)!		2

	6 2		6!
|A|=		=		=15
			2!*4!

	15
P(A)=
	(n−1)n   2

15		1
	<		→ rozwiąż tę nierówność...
(n−1)n   2		3

Gustlik: W tego typu zadaniach z nierównościami może wyjść ułamek, rozwiązanie nierówności może być np. n>10,5, co dla liczb naturalnych znaczy to samo, co n>10. Gdyby polecenie brzmiało "Dla jakich wartości n prawdopodobieństwo tego, że dwa zakupione kalkulatory są wadliwe jest równe

	1
		", wtedy musiałbys ułożyć równanie, zamiast nierówności i odpowiedź musiałaby wyjść np.
	3

n=10, a więc wtedy ułamek nie mógłby wystapić, bo nie może być np. 10,5 kalkulatora. Ale w przypadku nierówności może tak być, widocznie przy n=10 P(A)>1/3, a przy n=11 P(A)<1/3.

Aga: bleek można i tak jak zacząłeś, tylko wszystkich kalkulatorów jest n. w tym 6 wadliwych, a n−6 sprawnych.

6		5		1
	*		<
n		n−1		3

po rozwiązaniu n>10.

Bleek: Gustlik− dzieki za wytlumaczenie i zadania i mozliwosci odpowiedzi. wole nie robic tych zadan kombinatoryka. co prawda przerabialem ja, ale na prostszych zadaniach, tym bardziej ze matematyke mam na podstawie. Aga− od razu zrobilbym tak jak Ty, ale w ksiazce mam podobne zadanie, w ktorym jest n ksiazek W TYM 7 w jezyku angielskim i jest ⁷_n+7 i ⁿ_n+7. nie wiem czy autorzy myla czy jak. w kazdym razie odpowiedz wychodzi dobra wiec skorzystam z Twojego rozwiazania. Dzieki wam obu ponownie!

Bleek: Gustlik− dzieki za wytlumaczenie i zadania i mozliwosci odpowiedzi. wole nie robic tych zadan kombinatoryka. co prawda przerabialem ja, ale na prostszych zadaniach, tym bardziej ze matematyke mam na podstawie. Aga− od razu zrobilbym tak jak Ty, ale w ksiazce mam podobne zadanie, w ktorym jest n ksiazek W TYM 7 w jezyku angielskim i jest ⁷_n+7 i ⁿ_n+7. nie wiem czy autorzy myla czy jak. w kazdym razie odpowiedz wychodzi dobra wiec skorzystam z Twojego rozwiazania. Dzieki wam obu ponownie!