Prosze o rozwizanie gabi: Prosze o pomoc w rozwiązaniu tych dwóch zadan. Graniastosłup ma 2n+6 wierzchołków.Liczba wszystkich krawedzi tego graniastoslupa jest równa w odpowiedzi wynosi to :3n+9 (jak do tego dość) Tworząca stożka jest o 2 dłuższa od promienia podstawy.Pole powierzchni bocznej tego stożka jest równa 15π .Tworzaca stożka ma zatem długość.Odp.jest to 5(jak do tego dość)

Gustlik: ad 1). Wzory na liczbę krawędzi K, wierzchołków W, ścian bocznych S_b i wszystkich ścian S graniastosłupa N−kątnego: K=3N W=2N S_b=N S=N+2 W=2n+6 2N=2n+6 /:2 N=n+3 − jest to graniastosłup (n+3)−kątny K=3N K=3(n+3)=3n+9

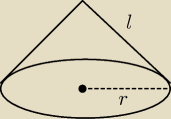
Gustlik: Tworząca stożka jest o 2 dłuższa od promienia podstawy.Pole powierzchni bocznej tego stożka jest równa 15π .Tworzaca stożka ma zatem długość.Odp.jest to 5(jak do tego dość) P_b=15π l=r+2 "Co masz dane, to obliczasz", masz dane pole boczne, więc je obliczasz na niewiadomych i przyrównujesz do podanego w zadaniu. P_b=πrl=πr(r+2) πr(r+2)=15π → rozwiąż teraz to równanie − obliczysz promień, a potem z niego tworzącą.