działania kasia:

x2−25		x2−36
	*
x2−6x		x2−4x−5

Eta: założenia: x≠0, x≠6, x≠−1, x≠ 5

(x−5)(x+5)		(x−6)(x+6)
	*		=......
x(x−6)		(x+1)(x−5)

kasia: właśnie tego nie rozumie

kasia: wytłumaczysz ?

krystek: masz rozłożone na czynniki x²−25=x²−5²=(x−5)(x+5) x²−6x=x(x−6) x²−36=x²−6²=(x−6)(x+6) a x²−4x−5 = (x−x₁)(x−x₂) liczysz Δ i x₁ i x₂

kasia: Δ=4²−4*1*(−5) Δ= 36

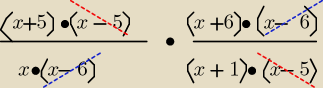Eta: Korzystasz ze wzoru: a²−b²= (a−b)(a+b) to: x²− 25= (x−5)(x+5) i podobnie x²−36= (x−6)(x+6) teraz mianowniki : x²−6x= x(x−6) bo wyłączamy x przed nawias x²−4x−5 Δ= 36 √Δ= 6 x₁= ..... x₂=..... to mamy rozkład ( x−x₁)(x−x₂) =..... dokończ

(x+5)(x−5)		(x+6)(x−6)
	*		= ..... po uproszczeniu
x(x−6)		(x+1)(x−5)

	(x+5)(x+6)
=
	x(x+1)

i to wszystko Czy już jasne?

kasia:

	4−√36
x1 =
	2

	4+√36
x2 =
	2

kasia: juz tak ale to co wszysniej napisałem to widze ze zle dzieki