natalka: Podstawą ostrosłupa jest kwadrat o boku długości 1 dm, a spodkiem wysokości ostrosłupa jest
jeden z wierzchołków tego kwadratu. Dwie ściany boczne są nachylone do płaszczyzny podstawy
pod kątem 60° oblicz: a) długość krawędzi bocznych b) pole powierzchni całkowitej tego
ostrosłupa
10 gru 17:43
natalka: może ktoś powiedzieć mi jak to zrobić'
10 gru 17:46
Aga: Zdaje się, że wczoraj było takie zadanie.
10 gru 17:54
natalka: tylko nikt konkretnie nie powiedział jak je zrobić
10 gru 18:34
dero2005:
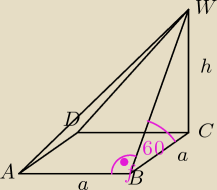
a = 1 dm
oznaczenia:
|BW| = |DW| = l
|AW| = l
1
h = a
√3 =
√3
l =
√a2 + h2 =
√12 + √32 =
√4 = 2
l
1 =
√a2 + l2 =
√12 + 22 =
√5
ściany boczne są trójkątami prostokątnymi i tak:
− ściana BCW = DCW powierzchnia tych ścian wynosi a*h =
√3
− ściana ABW = ADW powierzchnia tych ścian wynosi a*l = 2
− podstawa ABCD jest kwadratem powierzchnia wynosi a
2 = 1
Całkowita powierzchnia ostrosłupa wynosi więc
P
c =
√3 + 2 + 1 = 3 +
√3 dm
2
10 gru 20:03
natalka: dlaczego IAWI= I1I

?
10 gru 21:22
dero2005:
odcinek |AW| jest najdłuższą krawędzią boczną ostrosłupa i nazwałem go l1 (l − jak ludwik)
jego długość wynosi √5 dm
10 gru 21:31
Grześ: niewiem
25 kwi 22:41
 a = 1 dm
oznaczenia:
|BW| = |DW| = l
|AW| = l1
a = 1 dm
oznaczenia:
|BW| = |DW| = l
|AW| = l1
 ?
?