geometria analityczna ewka1114: Dany jest okrag o równaniu (x−3)²+y²=36 Punkt A=(3,−6) jest wierzchołkiem trójktą równobocznego wpisanego w dany okrag. Wyznacz współrzędne wierzchołków B i C

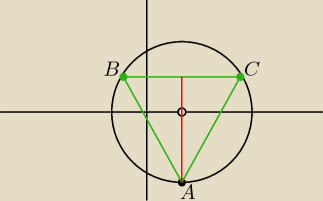
-:): ... znasz promień okręgu ... znasz więc i długość boku trójkąta Odcinek AC ma więc określoną długość a jednocześnie współrzędne punktu C spełniają równanie okręgu A można i sprytniej ... Wyznacz równanie prostej przechodzącej przez punkty A i B (wykorzystując znaną wysokość trójkąta) Później poszukaj punktów przeciącia się tej prostej z okręgiem.

Basia: wyznacz S (środek okręgu) i R zrób rysunek pr.AS, w której zawiera się wysokość trójkąta || OY ⇒ pr.BC || OX czyli ma równanie y = b D − środek odc.BC D(3,b) R = ²₃h h = ³₂R AD = h z tego wyliczysz b a potem układ równań: y = b i równanie okręgu

ewka1114: w jaki sposób mam wyznaczyć z AD b ?

ewka1114: ok już wiem dziekuje !