zadania na kółko matematyczne w gimnazjum pilna pomoc żanecia15: Pole powierzchni całkowitej prostopadłościanu wynosi 50(1+√3)cm2. Przekątna jednej ścian bocznych jest nachylona do płaszczyzny podstawy pod kontem 45° ,a przekątna sąsiedniej ściany bocznej jest nachylona do płaszczyzny podstawy pod kontem 60°. Oblicz długość krawędzi tego prostopadłościanu

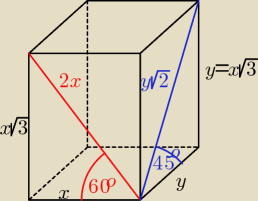
Gustlik: Jeżeli dane są takie wielkości, ktore zazwyczaj się liczy, jak pole czy objetość, to stosujemy zasadę "co masz dane to obliczasz i porównujesz". Mam dane pole, a więc obliczam to pole. P_c=P_b+2P_p P_b=L*H, gdzie L − obwód podstawy (wzór prawdziwy dla wszystkich graniastosłupów prostych − wystarczy narysować siatkę graniastosłupa, żeby go udowodnić) L=2x+2y=2x+2x√3 H=y=x√3 P_b=(2x+2x√3)*x√3=2x²√3+6x² P_p=xy=x*x√3=x²√3 P_c=2x²√3+6x²+2x²√3=4x²√3+6x²=2x²(2√3+3) 2x²(2√3+3)=50(1+√3) − rozwiąż teraz to równanie, obliczysz x, a z x pozostałe krawędzie. Mam jeszcze jedno pytanie: na pewno pole ma wynosić 50(1+√3), a nie 50(3+2√3)? Bo wtedy wyszedłby ładny wynik, a tak będzie zabawa z pierwiastkami.