pomozcie, nie wiem od czego zaczac. :| teefe: w trapezie równoramiennym przekątna ma długość 2√41 cm, zaś wysokość 8 cm. Oblicz pole tego trapezu i długość odcinka łączącego środki ramion.

Mila: C' spodek wysokości na dolnej podstawie ( nie mogę opisać rysunku)

	a+b
AC' =		własność w trapezie równoramiennym
	2

AC'² = 4∧41−64 z tw. PItagorasa AC'= 10 P = 10 ∧ 8

	a+b
Odcinek łączący środki podstaw =		=10
	2

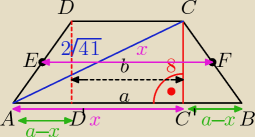
Gustlik: Z ΔABC': (2√41)²=x²+8² 4*41=x²+64 164−64=x² x²=100 x=10 a=b+2(a−x) a=b+2a−2x 2x=b+2a−a 2x=a+b /:2

	a+b
x=		, taki sam jest wzór na odcinek łączący środki ramion, można udowodnić to z tw.
	2

Talesa. Zatem |EF|=x=10

	(a+b)h
Pole =		=xh=10*8=80
	2

Gustlik: Mały chochlik: w pierwszym wierszu powinno być: Z ΔAC'C, reszta jest dobrze.