Prosze o pomoc w zadaniach na jutrzejsze zalicznie semestru
XxX: Podstawą ostrosłupa prostego jest trójkąt równoramienny, którego dwa boki mają długość 17 cm i
16 cm. Wszystkie krawędzie boczne są nachylone do płaszczyzny pod kątem ostrym α takim, że
sin α =√2/2.oblicz wysokość tego ostrosłupa
9 gru 19:34
dero2005:
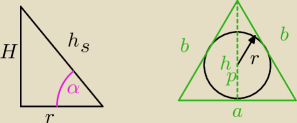
jeżeli trójkąt jest równoramienny i podane są dwa boki mają 16 i 17 cm to
może być tak, że podstawa jest równa 16 cm a ramiona po 17 lub podstawa 17 a ramiona po 16.
Należy policzyć h
p z Pitagorasa potem promień r ze wzoru
α = 45
o
H = r
9 gru 20:23
Aga: Jeśli wszystkie krawędzie są nachylone pod kątem α, to spodek wysokości ostrosłupa jest
środkiem okręgu opisanego na podstawie.
α=45
0 , H=R, gdzie
a=16 , b=c=17
Z Pitagorasa h podstawy = 15
9 gru 21:31
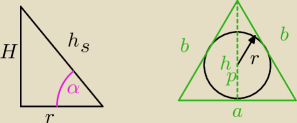 jeżeli trójkąt jest równoramienny i podane są dwa boki mają 16 i 17 cm to
może być tak, że podstawa jest równa 16 cm a ramiona po 17 lub podstawa 17 a ramiona po 16.
Należy policzyć hp z Pitagorasa potem promień r ze wzoru
jeżeli trójkąt jest równoramienny i podane są dwa boki mają 16 i 17 cm to
może być tak, że podstawa jest równa 16 cm a ramiona po 17 lub podstawa 17 a ramiona po 16.
Należy policzyć hp z Pitagorasa potem promień r ze wzoru