ostrosłup betka: Czy może ktoś sprawdzić mi to zadanie Oblicz miarę kąta dwuściennego przy podstawie ostrosłupa prawidłowego trójkątnego, jeśli: A) wysokość ostrosłupa jest trzy razy krótsza od wysokości podstawy B) wysokość ostrosłupa jest dwa razy krótsza od krawędzi podstawy A) tg∡α=1/3*3= 1 tg∡α=45° ∡α=45° b) 1/3*(a√3)/2=(a√3)/2 Tg∡α=1/2*(6/a√3)=√3 Tg∡α= 60° ∡α=60°

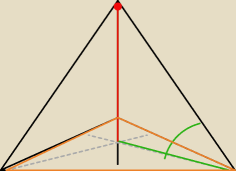
krystek: Kąt dwuścienny jest między pł ściany a pł podstawy. A Ty zaznaczony masz kąt nachylenia krawędzi bocznej do pł podstawy. Czy to jest prawidłowyΔ ostrosłup?

kylo1303: zadanko zrobione źle. wysokosc ostroslupa dzieli wysokosc podstawy w stosunku 1:2. Dodatkowo nie wiem co oznacza: 1/3*(a√3)/2=(a√3)/2, to jest sprzecznosc. Plus to co pisał krystek

sushi_ gg6397228: A) to dlaczego liczysz ze wysokosc bryly=== wysokosc podstawy

kylo1303: Wyniki sie zgadzaja, ale chyba mialas je podane i probowalas "dorobic" zadanie do wyniku, nastepna niescislosc:

	√3
1/2*(6/a√3)=√3 gdzie podzialo sie a? 1/2*(6/a√3)=
	a

betka: Tg∡α=1/2a*(6/a√3)=√3