Dziedzina funkcji
niko:
Dziedziną funkcji f(x) = x+2
−−−−−−−
x
2−4
Jaki jest zbiór i dlaczego
9 gru 00:55
ZKS:
x2 − 4 ≠ 0 ponieważ nie można dzielić przez 0.
9 gru 00:56
niko: znaczy chodzilo mi o to w jakim zbiorze się będzie to znajdować w książce w odpowiedziach pisze
ze
(−
∞;−2) ∪ (−2;2) ∪(2; +
∞)
A ja nie wiem jak to rozwiązać przy tablicy gdyż dwa tygodnie mnie nie było w szkole z powodu
choroby a jutro będę pytana z tego
9 gru 01:02
Tarkus: a napisałeś wszystko nie ma tam większe lub mniejsze od czegoś
9 gru 01:16
Tarkus: sry za (łeś) późno już
9 gru 01:20
ZKS:
Nie musisz pisać przedziałów wystarczy że wyrzucisz liczby które nie należą do dziedziny ze
zbioru liczb rzeczywistych.
x2 − 4 ≠ 0
(x − 2)(x + 2) ≠ 0
x ≠ ±2
Df = ℛ \ {±2}.
9 gru 01:20
niko: | | x+2 | |
pisze ze Dziedziną funkcji f(x)= |
| jest zbiór : Jest kilka odp no i własnie z tyłu |
| | x2−4 | |
ksiązki pisze, że (−
∞;−2) ∪ (−2;2) ∪(2; +
∞)
9 gru 01:22
Tarkus:
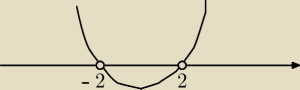
(x+2)(x
2−4) ⇔ (x+2)(x+2)(x−2)
x=−2 x=−2 x=2
X∊ (−
∞,−2)U(−2,2)U(2,+
∞)
ja tak bym to zrobił
9 gru 01:27
ZKS:
Tarkus w ogóle nie wiem Co Ty zrobiłeś trzeba ustalić dziedzinę a nie rozwiązywać
nierówności.
9 gru 01:31
ZKS:
Zbiór liczb rzeczywistych to (−∞ ; ∞) do naszej dziedziny nie należą liczby ±2 więc je
wyrzucamy i powstają na dziury (−∞ ; −2) ∪ (−2; 2) ∪ (2 ; ∞) i to jest właśnie nasza
dziedzina.
9 gru 01:32
niko: jej wielkie dzięki !
A mam jeszcze jedną prośbę powiesz mi jak zrobić to zadnie:
Dana jest funkcja określona wzorem f(x)=|x−3|. Sporządź tabelę dla kilku wybranych argumentów,
a następnie naszkicuj wykres funkcji f. Ustal zbiór wartości funkcji oraz podaj argumenty, dla
których funkcja przyjmuje wartość 0.
Wiem, że to moze głupie pytanie ale jak mówiłam nie wiem o co kompletnie chodzi gdyż 2 tyg w
szkole mnie nie było a z maty zawsze słaba jestem
9 gru 01:33
Tarkus: narysowałem wykres tej funkcji i z wykresu napisałem dziedzinę nie można tak?
9 gru 01:33
ZKS:
9 gru 01:36
ZKS:
niko wiesz jak wygląda wykres funkcji f(x) = |x| ?
9 gru 01:37
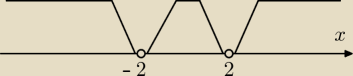
ZKS:
Tamto co narysowałem to do zobrazowania jak wygląda dziedzina.
9 gru 01:38
ZKS:
| | x + 2 | |
Trakus wykres funkcji f(x) = |
| wygląda zupełnie inaczej Ty narysowałeś |
| | x2 − 4 | |
parabolę a ten wykres jest hiperbolą.
9 gru 01:40
Tarkus: ZKS ale ta funkcja dla x = 1 będzie −1 tak? a Ty masz wartości tylko dodatnie czy ja coś źle
rozumiem
9 gru 01:45
ZKS:
Wiesz jak wygląda f(x) = |x|? Czekam 5 min na odpowiedź jeżeli nie napiszesz to idę spać.
9 gru 01:45
Tarkus:
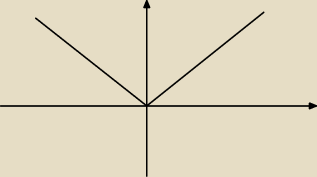
9 gru 01:46
niko: Wybaczcie net mi padł.
Nie nie mam pojęcia
9 gru 01:46
ZKS:
Źle rozumiesz narysowałem dziedzinę funkcji w postaci osi x w przedziale od (−∞ , ∞) i
wyrzucając po drodze liczby nie należące do niej.
9 gru 01:47
Tarkus: aha ok a mógłbyś tak poglądowo narysować jak powinien wyglądać?
9 gru 01:48
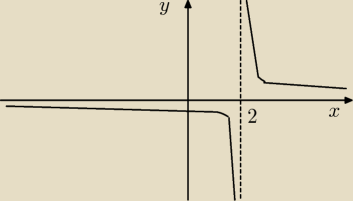
ZKS:
Z tą funkcją
Tarkus mogę się zgodzić.
f(x) = |x| teraz przesuwamy ten wykres o 3
jednostki w prawo i dostajemy wykres g(x) = |x − 3|.
9 gru 01:50
ZKS:
Spróbuję.
9 gru 01:50
ZKS:
9 gru 02:02
Tarkus: dzięki za czas
9 gru 02:04
ZKS:
Nie ma za co od tego jest to forum.
9 gru 02:05
niko: Tak ja tez bym chciała podziękowac
9 gru 02:06
Tarkus: chyba musisz jeszcze narysować niko ten wykres bo chyba nie bardzo wie jak ma to wyglądać
9 gru 02:06
ZKS:
niko wiesz jak narysować ten wykres |x − 3| teraz czy nadal nie?
9 gru 02:11
niko: wiem wiem
9 gru 02:14
niko: Dobra ja mykam bo o 6 trzeba wstac
Jeszcze raz wielkie dzieki za pomoc w zadniu ^^
9 gru 02:15
ZKS:
Na zdrowie.
Dobrze że jutro mam na 10.
9 gru 02:20
Aga: | | x+2 | | 1 | |
ZKS źle narysowałeś wykres funkcji f(x)= |
| .= |
| , gdy x≠−2 i x≠2 |
| | x2−4 | | x−2 | |
Będzie hiperbola z "dziurką", bo do dziedziny nie należy też x=−2.
10 gru 11:11