rozwiązać równość i nierówność
Tarkus: a)
x
2−|x|=0
czy to będzie tak?
x
2−x=0 Δ=1
√Δ=1 x
1=1 x
2=0 ?
| | x−1 | | 1 | |
b) |
| >−2 x∊(−∞,−1) U (− |
| ,+∞) |
| | x+1 | | 3 | |
mógłby ktoś sprawdzić czy dobrze?
9 gru 00:39
załamany :(: w pod a bym rozpatrywał dwa przypadki.
9 gru 00:47
asik: tak gdy x≥0 lub x2+x=0 gdy x<0 czyli x=−1 jest również pierwiastkiem
9 gru 00:47
Tarkus: obliczyc granice ciagow i funkcji
a)n→
∞ n√7n+10n granica 10 ?
| | 2n−3 | | 1 | |
b)n→∞ ( |
| )3n granica |
| ? |
| | 2n+5 | | e12 | |
c)x→+
∞ x
2−
√x4+2 granica 0 ?
9 gru 00:48
załamany :(: waszak −1 tez spełnia to równanie
9 gru 00:48
Tarkus: czyli w a x∊{1,0,−1} tak?
9 gru 00:50
załamany :(: tak
9 gru 00:50
Tarkus: proszę sprawdźcie następne
9 gru 00:52
9 gru 00:55
Tarkus: a nie równość z pierwszego postu?
9 gru 00:55
ZKS:
W porządku.
9 gru 00:59
Tarkus:
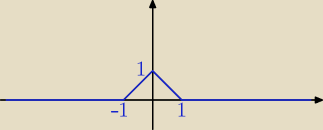
jeszcze mam taki wykresik
0 dla x<−1
f(x)= x−1 dla <−1,0>
−x+1 dla <0,1>
0 dla x>1
9 gru 01:01
Tarkus: tam jest x+1 dla <−1,0>
9 gru 01:05
Tarkus: jest ok?
9 gru 01:11
ZKS:
9 gru 01:11
Tarkus: dzięki wielkie chłopaki
9 gru 01:12