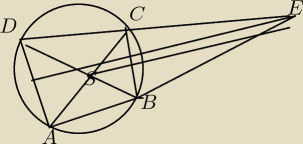
POMOCY geometria asik: POMOCY Wykaż ze dwusieczna kąta AED jest równoległa do dwusiecznej kąta CSB, gdzie S jest punktem przecięcia się przekątnych czworokąta ABCD wpisanego w okrąg ,a E jest punktem przecięcia się przedłużeń boków AB i CD

Andrzej: Pewnie jest prostszy sposób, ale ja zrobiłem tak "na piechotę" bo już późno i myślenie nie takie... ale wyszło. Przekątne czworokąta ABCD tworzą z jego bokami osiem kątów, ale tam są pary kątów przystających (wpisane, oparte na tym samym łuku), więc do ich oznaczenia wystarczą Ci cztery literki (α,β,γ,δ). Teraz wylicz przy pomocy tych literek kąty, jakie każda z dwusiecznych tworzy z bokiem CD. (Wykorzystaj sumy kątów w trójkątach ECB i SCB). Wyjdzie, że te kąty są równe, czyli że te dwusieczne są równoległe.

asik:

asik: Andrzejku dzięki

asik: może ktoś ma inny pomysł na rozwiązanie

asik:

asik : Coś mi tu nie pasuje .Może ktoś mi pomóc

Andrzej: Mogą Ci nie pasować literki z mojego rozwiązania, bo na moim rysunku punkt E był po lewej stronie okręgu. Według rysunku który zrobiłaś, będzie: "Teraz wylicz przy pomocy tych literek kąty, jakie każda z dwusiecznych tworzy z bokiem AD. (Wykorzystaj sumy kątów w trójkątach EAD i SCB). Wyjdzie, że te kąty są równe, czyli że te dwusieczne są równoległe."

Andrzej: Heh, jeszcze raz, bo już mi się literki pomieszały: "Teraz wylicz przy pomocy tych literek kąty, jakie każda z dwusiecznych tworzy z bokiem AD. (Wykorzystaj sumy kątów w trójkątach EAD i SAD). Wyjdzie, że te kąty są równe, czyli że te dwusieczne są równoległe."

asik : proszę podaj mi pełne rozwiązanie coś mi się nie zgadza