Ostrosłupy Alicja: Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, wiedząc, że jego wysokość jest równa 4√3 i tworzy z krawędzią boczną kąt 30 stopni. Prosiłabym o rozwiązanie i wyjaśnienie, abym mogła przeanalizować zadanie. Z góry bardzo serdecznie dziękuję!

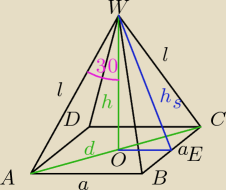
dero2005: h = 4√3 rozpatrujemy trójkąt AOW

h		√3
	= cos 30o =
l		2

	2√3h		2√3*4√3
l =		=		= 8 → krawędź boczna
	3		3

z Pitagorasa

d
	= √l2 − h2 = √82 − (4√3)2 = √64 − 48 = √16 = 4
2

d = 2*4 = 8 → przekątna podstawy rozpatrujemy trójkąt ABC d² = 2a²

	d√2		8√2
a =		=		= 4√2 → krawędź podstawy
	2		2

rozpatrujemy trójkąt ECW (Pitagoras) h_s = √l² − (^a₂)² = √8² − (2√2)² = √64 − 8 = √56 = 2√14 → wysokość ściany bocznej P_p = a² = (4√2)² = 32 → pole podstawy

	a*hs
Pb = 4*		= 2*a*hs = 2*4√2*2√14 = 32√7 → pole boczne
	2

P_c = P_p + P_b = 32 + 32√7 = 32(1+√7) → pole całkowite

	1		1		128
V =		Pp*h =		*32*4√3 =		√3 → objętość
	3		3		3