podział koła na części IQ75: witam. mam problem, mianowicie potrzebuje podzielić koło dwiema cięciwami równoległymi do siebie tak aby wszystkie trzy powstałe figury miały takie samo pole powierzchni. z góry dziękuje

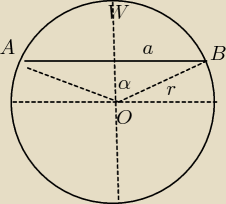
AS: Zakładam,że jest dany promień koła r. Pole odcinka ABW = Pole wycinka OAWB − Pole trójkąta AOB

	1
Pole wycinka Pw =		r2*2*α = r2*α α w radianach
	2

	1
Pole trójkąta Pt =		*r2*sin(2*α)
	2

Z warunku postawionego w zadaniu

	1		1
r2*α −		*r2*sin(2*α) =		π*r2 |:r2
	2		3

	1		1
α −		*sin(2*α) =		*π
	2		3

Rozwiązaniem tego równania jest α = 1.92023 [rad] = 110 [st] 1 [min] Mając wyliczone α obliczymy a = r*sin(α) i resztę potrzebnych elementów.

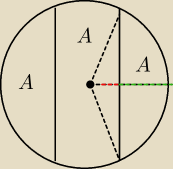
IQ75: tak w zadaniu mamy dany promień tego koła. niestety to co opisałeś nie zgadza się, to nie może być kat 110stopni, po wykonaniu rysunku już widać że musi być większy. może niedokładnie sformułowałem zadanie. teraz jest rysunek może to pomoże. chodzi albo o kąt tak jak przedtem podałeś, lub stosunek podziału promienia. A − oznacza obszary o takim samym polu.

AS: Masz rację,kropnąłem się w przepisywaniu błędnej danej. Poprawny wynik (sprawdzony) α = 1.30266 [rad] = 74 [st] 38 [min] , a cały kąt środkowy: 149 [st] 16 [min] Przepraszam za pomyłkę.

IQ75: dzięki, jesteś Mistrz