rzzucamy kostką i liczymy zdarzenia Jonaszek: Cześć! czy byłby ktos tak miły i sprawdził mi poniższe zadanie z prawdopodobieństwa rzucamy dwoma kostkami jednocześnie A oznacza zdarzenie że suma oczek jest równa 5 B oznacza zdarzenie w którym przynajmniej na jednej kostce wypadła parzysta liczzba oczek opisz zdarzenia a∩b ; a∪b ; B/A ; A/B ; B' zrobiłem coś takiego Ω=6*6=36 A (1,4) ; (2,3) ; (3,2) ; (4,1) P(A)=4/36=1/9 B (1,2) ; (1,4) ; (1,6) (2,1) ( 2,2) (2,3) (2,4) (2,5) (2,6) (3,2) (3,4) (3,6) (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) (5,2) (5,4) (5,6) 6,1) (6,2) (6,3) (6,4) (6,5) (6,6) p(B)=27/36=3/4 gdzies podobnym zadaniu wyczytałem że jako że zdarzenie A sprzyja równocześnie z B to P(A∩B)=4/36=1/9 P(A∪B)=1/9 + 3/4 − 1/9 = 4/36 + 27/36 − 4/36 = 27/36 = 3/4 P(b') = 1−P(B) = 1/4 P(B/A)= 3/4 * 9/1 = 27/4 <−−− w ogóle może wyjśc taka liczba ? P(A/B) = 1/9 * 4/3 = 4/27 mógłby mnie ktos naprowadzić na włąściwą scieżkę?

Aga: Czy masz obliczyć prawdopodobieństwo warunkowe, czy różnicy? Dwie ostatnie linijki są źle.

Jonaszek: prawdę mówiąc to nie mam pojęcia polecenie brzmi j/w

Aga:

	P(A∩B)
P(A/B)=		→prawdopodobieństwo zajścia zdarzenia A pod warunkiem, że zaszło
	P(B)

zdarzenie B.(ta kreska raczej powinna być pionowa) P(A−B)=P(A)−P(A∩B).→prawdopodobieństwo różnicy zdarzeń A i B

Jonaszek: no i przyjmując że chodzi o prawdopodobienństwo warunkowe to niby dobrze liczyłem tak? ¹₉ * ⁴₃ = ⁴₂₇ czy we wcześniejszym etapie na pewno wszystko poprawnie zrobiłem?

Aga: Druga linijka jest źle .

1		9
	*		=1
9		1

Jeśli prawdopodobieństwo warunkowe, to ostatnia dobrze.Wydaje się, że reszta dobrze.

Mila: Zbiór B\A oznacza zawiera tylko te elementy zbioru B, które nie są wspólne z A, ma zatem 27− 4 elementów, podobnie Zbiór A\B (jest on pusty) Natomiast prawdopodobieństwo warunkowe. P(A/B) = 4/27 ( moc zbioru A∩B podzielone przez moc zbioru B) P(B/A)= 1 ( moc zbioru A∩B podzielone przez moc zbioru A)

Gustlik: rzucamy dwoma kostkami jednocześnie A oznacza zdarzenie że suma oczek jest równa 5 B oznacza zdarzenie w którym przynajmniej na jednej kostce wypadła parzysta liczzba oczek opisz zdarzenia a∩b ; a∪b ; B/A ; A/B ; B' |Ω|=6*6=36

	4		1
A={(1, 4), (2, 3), (3, 2), (4, 1)}⇒|A|=4⇒P(A)=		=
	36		9

B−przynajmniej na jednej kostce wypadła parzysta liczzba oczek⇒ B'− na obu kostkach wypadła nieparzysta liczba oczek

	9		1		3		27
|B'|=3*3=9, P(B')=		=		⇒P(B)=		=
	36		4		4		36

	4		1
A∩B={(1, 4), (2, 3), (3, 2), (4, 1)}⇒|A∩B|=4⇒P(A∩B)=		=
	36		9

	4		27		4		27		3
P(AUB)=P(A)+P(B)−P(A∩B)=		+		−		=		=
	36		36		36		36		4

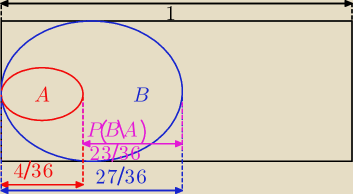
	27		4		23
P(B\A)=		−		=		− można odczytać to z rysunku
	36		36		36

P(A\B)=0 − zbiór pusty