dowód tn: Witam, jak w najprostszy sposób udowodnić że: promień okręgu do którego poprowadzono styczną pada na nią pod kątem prostym

nieokiełznany: równanie prostej przechodzącej przez srodek okregu i jakiś punkt A należący do okręgu y = ax + b₁ równanie prostej przechodzącej przez punkt A styczny do okręgu

	1
y = −		x + b2
	a

Mila: Styczna jest odległa od środka okręgu o długość promienia. Odległość punktu od prostej mierzymy po prostopadłym odcinku.

lokol:

ziutek: jakies inne pomysly?

tn:

Basia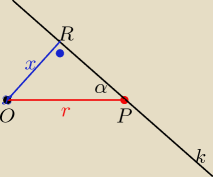: O − środek okręgu P − punkt styczności k − styczna (?), która nie jest ⊥ do odc.OP α≠90 wtedy: istnieje prosta prostopadła do k przechodząca przez punkt O i nie jest to prosta k (na rysunku pr.OR) ⇒ tr.ORP jest prostokątny ⇒ OR < OP=r ⇒ punkt R leży wewnątrz okręgu ⇒ k nie jest styczną c.b.d.o.

Basia: dokładniej jeszcze ⇒ istnieje na prostej k punkt S taki, że S≠P i RS = RP = r ⇒ S, P ∊k i ∊okręgu ⇒ k nie jest styczną

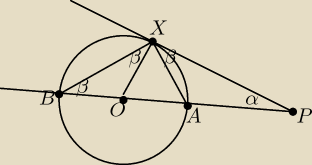Vax: Mamy pokazać, że jeżeli do okręgu poprowadzimy styczną, to promień poprowadzony do tej stycznej będzie tworzył z nią kąt 90*, a nie, że jeżeli pewna sieczna nie tworzy z promieniem 90* to nie jest styczną, to nie implikuje naszej tezy. Poprowadźmy z pewnego punktu P styczną PX do naszego okręgu o środku O. Dodatkowo niech prosta PO tnie okrąg odpowiednio w punktach A,B. Oczywiście wtedy AB jest średnicą, czyli <BXA = 90*. Z twierdzenia o siecznej dostajemy:

	|PA|		|PX|
|PX|2 = |PA|*|PB| ⇔		=		czyli ΔPAX ~ ΔPBX, stąd <AXP = <PBX = <BXO =
	|PX|		|PB|

β. Czyli 90* = <BXA = <BXO+<OXA = <AXP+<OXA = <OXP cnd.