proszę o pomoc
zuza1325: w trójkącie KLM K=(−1;1), L =(2;5), M=(−2;3)
a) wyznacz równania boków tego trójkąta
b) oblicz jego pole i obwód
c) napisz równanie symetralnej boku LM
d) napisz równanie środkowej boku LM
7 gru 22:46
zuza1325: d )mam zrobione tak
S= ((X1+X2)/2, (Y1+Y2)/2)
S=((2+(−2))/2, (5+3)/2)
S= (0,4)
7 gru 22:50
krystek: Wyznaczyłas środek boku a nie środkową!
7 gru 22:59
7 gru 23:00
7 gru 23:06
Gustlik: Można prościej:
| | yB−yA | |
a= |
| − to wzór na wspólczynnik kierunkowy prostej przechodzącej przez 2 |
| | xB−xA | |
punkty. Obliczamy a, wstawiamy do funkcji liniowej y=ax+b, potem podstawiamy współrzędne
jednego z tych punktów i po sprawie.
ad a)
Dla przykładu wyznaczę równanie boku LM:
L=(2, 5)
5=1+b
b=4
Pozostałe robisz podobnie.
8 gru 00:00
Gustlik:
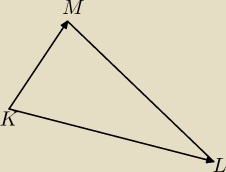
ad b) pole i obwód:
K=(−1;1), L =(2;5), M=(−2;3)
Z dwóch boków robisz wektory tak, żeby miały wspólny początek, np. w punkcie K, jak na rysunku.
Liczysz teraz współrzedne tych wektorów:
KL
→=L−K=[2−(−1), 5−1]=[3, 4]
KM
→=M−K=[−2−(−1), 3−1]=[−1, 2]
Liczysz teraz wyznacznik tych wektorów (patrz:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 )
d(KL
→, KM
→)=
| 3 4 |
| −1 2 |
=3*2−4*(−1)=6+4=10
| | 1 | | 1 | |
Odp: Pole = |
| |d(KL→, KM→)|= |
| *|10|=5 |
| | 2 | | 2 | |
Obwód:
Liczę współrzędne wektora LM
→ (trzeci bok)
LM
→=M−L=[−2−2, 3−5]=[−4, −2]
Liczę długości tych trzech wektorów:
|KL|=
√32+42=
√9+16=
√25=5
|KM|=
√(−1)2+22=
√1+4=
√5
|LM|=
√(−4)2+(−2)2=
√16+4=
√20=2
√5
Odp: Obw=5+
√5+2
√5=5+3
√5
8 gru 00:10
Gustlik: w trójkącie KLM K=(−1;1), L =(2;5), M=(−2;3)
ad c) napisz równanie symetralnej boku LM
Środek tego boku S=(0, 4) skorzystam z Twojego obliczenia, bo jest dobre.
| | 1 | |
Wspólczynnik kierunkowy boku LM: a= |
| (patrz: ad a)) |
| | 2 | |
Współczynnik kierunkowy symetralnej (prosta prostopadła) a
2=−2
y=−2x+b
Podstawiasz współrzędne S:
4=−2*0+b
b=4
Odp: y=−2x+4
8 gru 00:13
Gustlik:
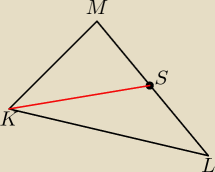
W trójkącie KLM K=(−1;1), L =(2;5), M=(−2;3)
d) napisz równanie środkowej boku LM
Czy to ma być tak jak na rysunku? Bo jest niejasno sprecyzowane polecenie.
Jeżeli tak, to:
K=(−1; 1)
S=(0; 4)
Liczysz tak jak pkt. a) − prosta przechodząca przez 2 punkty K i S.
y=3x+b
4=3*0+b
b=4
Odp: y=3x+4
8 gru 00:20
Eta:
@
Gustlika
Można wykazać,że trójkąt KLM jest prostokątny
(2
√5)
2+(
√5)
2= 5
2
20+5=25
| | 1 | |
zatem P(ΔKLM)= |
| *√5*2√5= 5 |
| | 2 | |
podobnie wykorzystać ten fakt przy wyznaczeniu równań prostych zawierających boki
oraz symetralną
Pozdrawiam

8 gru 00:55
Gustlik: Eta, Można, tylko po co się w to bawić? Jest prosty ogólny wzór wektorowy na pole i nie
trzeba kombinować jak koń pod górę, zwłaszcza, że nie było takiego polecenia w zadaniu. Poza
tym prostopadłość można wykazać iloczynem skalarnym − narysować ten trójką, wówczas z rysunku
będzie widać, który kąt może być prosty, obliczyć iloczyn skalarny wektorów tworzących ten kąt
(powinien wyjść 0) − jest prościej.
8 gru 01:05
Eta:
Nie zgadzam się z Tobą : "po co się w to bawić? " w co się bawić?
W tym przypadku , to prostsza metoda od tej co podajesz i czas zaoszczędzony!
Po wyznaczeniu długości boków w prosty sposób udowadniasz,że trójkąt jest prostkokątny
Pole wyznaczasz
błyskawicznie 
i równanie prostych prostopadłych też !
Koniec tematu

8 gru 01:23
Gustlik: Tylko trzeba to ZAUWAŻYĆ

! A nie każdy na to wpadnie, jak w poleceniu tego nie ma. Podałem
wektorową metodę obliczania pola, bo jest uniwersalna i prosta i pasuje do każdego przypadku.
8 gru 01:25
Gustlik: Poza tym do tego "błyskawicznego" wyznaczenia pola musisz i tak wyznaczyć długości boków (czyli
wektorów) więc nie jestem pewien, czy jest to mniej roboty.
8 gru 01:28
Eta:
Gustlik
Już kiedyś Ci pisałam i jeszcze raz przypomnę:
Nie musisz mnie uczyć ..... bo ja już to znałam, wtedy kiedy Ty
bawiłeś się jeszcze klockami w przedszkolu

Miłych snów

8 gru 01:30
Gustlik: Eta, ja wiem, że to znasz i umiałaś wcześniej niż ja, ale chciałem Cie uświadomić, że
Twoja "błyskawiczna" metoda wcale nie jest bardziej "błyskawiczna" od mojej. Pozdrawiam

8 gru 02:23
Aga: Wszystko zależy od etapu kształcenia.
a) Można wykorzystać wzór na równanie prostej przechodzącej przez dwa punkty lub wykorzystać
postać kierunkową prostej i ułożyć układ równań wyliczając a i b.
8 gru 07:47
krystek: Gustlik nikt tak jak Ty nie narzuca swego myślenia



!
Nie zniewalaj, nie narzucaj ! ucz uczniów logicznego myślenia!
Przeczytaj uważnie co napisała
Aga!
8 gru 09:41
Gustlik: @
Krystku − ja nikomu nie narzucam swojego sposobu myślenia, jedynie pokazuję NAJKRÓTSZĄ
DROGĘ rozwiązywania zadań, których w szkołach NIE MA, a za moich szkolnych czasów one w
większości były. Metodyka nauczania matematyki w szkołach to jest jazda z Warszawy do Łodzi
przez Pekin, przez to potem 21 % oblało mature z matmy, już nie raz o tym pisałem. Co do
Agi − te dwie metody to akurat najdłuższe metody znajdywania równania prostej
przechodzącej przez 2 punkty.
Najprostszy sposób to:
y=ax+b
Gdy x
B=x
A − wychodzi dzielenie przez 0, czyli wsp. kierunkowy a nie istnieje ⇒ prosta
"pionowa" o równaniu x=x
A − nie jest funkcją.
Gdy y
B=y
A − wychodzi a=0, mamy funkcję stałą − prosta "pozioma" y=y
A.
Proste jek drut − moi uczniowie ten sposób najbardziej lubią. Oczywiście pokazuję im, że wzór
się wziął właśnie z układu równań, tylko rozwiązałem układ na ogólnych danych.
Natomiast wzór na równanie prostej przechodzącej przez 2 punkty to nic innego jak rozbudowany
wzór (*) w trudno strawnej postaci, którą ciężko zapamiętać i nawet ja chcąc go zastosować
musiałbym za każdym razem zaglądać do tablic albo go sobie wyprowadzać. Natomiast wzorem (*)
robi się wszystko z pamięci, bo jest łatwy.
Pozdrawiam

8 gru 22:45
krystek: Jak grochem o ściane!
9 gru 09:31
Eta:
Jak widać "upierdliwości" nie da się wyleczyć

9 gru 20:11
Gustlik: @
Eta, z całym szacunkiem nie ja tym razem zacząłem. Podałem sposób na proste rozwiązanie
zadania, nikogo przy tym nie krytykując, sorry, ale tym razem Ty wyskoczyłaś jak Filip z
konopii. Masz jakąś alergię na mnie czy co

? A jeżeli chcesz wiedzieć, mam doświadczenie z
uczniami nie mniejsze niż Ty i wiem, jakie metody lepiej rozumieją, a na pewno krótkie i
przejrzyste metody, których ich uczę, wchodzą im do głowy lepiej niż szkolne tasiemcowe wzory
długie na dwie linijki czy uwielbiane przez nauczycieli układy równań z milionem niewiadomych
stosowane tam, gdzie z powodzeniem wystarczy równanie z jedną niewiadomą. Pozdrawiam Cię i
lepiej będzie jezeli zajmiemy się oboje pomaganiem innym, którzy tej pomocy od nas oczekują.

9 gru 23:28
krystek: @ Gustliku , pisałeś kiedyś ,że nie jesteś nauczyciele ,tylko zajmujesz sie korepetycjami
, nauczając nalezy uczniów zmuszać do myślenia !
10 gru 13:35
Gustlik: @P[Krystku]] Ja to właśnie robię

! Pokazuję zawsze, skąd wzięły się krótsze metody. Poza tym
co widzisz złego w nauczaniu prostszych metod? Dzięki temu uczniowie znają krótsze i logiczne
sposoby, zadania zajmują im mniej czasu, rozwiązując krótszym, przejrzystym i obrazowym
sposobem robią mniej błędów, a to zwiększa ich szanse na zdanie matury, bo na maturze niestety
liczy się czas. Uczeń znający krótkie metody zrobi dajmy na to trzy zadania, podczas gdy uczeń
"wyedukowany" (celowo w cudzysłowiu) topornymi i długimi szkolnym metodami w tym samym czasie
zrobi jedno zadanie, bo np. będzie przepisywał 20 razy równanie rozwiązując układ równań, mimo
że nie jest to potrzebne, będzie rozwiązywał zadanie z rzutu trzema kostkami drzewkiem i
rysował krzaka na całą kartkę A4, zamiast zastosować np. regułę mnożenia, będzie obliczał pole
trójkąta obliczając po kolei wszystkie odcinki, zamiast zrobić to wyznacznikiem wektorów i
ledwo wyciągnie, jak mu się uda, na te 30 %, bo więcej nie zdąży zrobić. A znając szybkie i
obrazowe metody ten sam uczeń zda maturę dajmy na to na 50 % i będzie lepiej rozumiał
zagadnienia.
Wiem, co u mnie zrobiono na prawdopodobieństwie w LO. Posadzono im te krzaki chyba korzeniem na
głębokości co najmniej 5 m pod ziemią, ja daję potem uczniowi zadanie z rzutem trzema
monetami, a on mi zaczyna dżunglę amazońską malować, zamiast zrobic to reguła mnożenia, co
zajęłoby mu 3 linijki i 2 minuty. I jak tu mówić o edukacji

? Drzewka to naprawdę świetna
metoda, ale do zadań z prawdopodobieństwa całkowitego, bez sensu jest stosować ją tam, gdzie
można wykonać proste obliczenia kombinatoryczne. Pozdrawiam.
10 gru 22:58
 ad b) pole i obwód:
K=(−1;1), L =(2;5), M=(−2;3)
Z dwóch boków robisz wektory tak, żeby miały wspólny początek, np. w punkcie K, jak na rysunku.
Liczysz teraz współrzedne tych wektorów:
KL→=L−K=[2−(−1), 5−1]=[3, 4]
KM→=M−K=[−2−(−1), 3−1]=[−1, 2]
Liczysz teraz wyznacznik tych wektorów (patrz: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 )
d(KL→, KM→)=
| 3 4 |
| −1 2 |
=3*2−4*(−1)=6+4=10
ad b) pole i obwód:
K=(−1;1), L =(2;5), M=(−2;3)
Z dwóch boków robisz wektory tak, żeby miały wspólny początek, np. w punkcie K, jak na rysunku.
Liczysz teraz współrzedne tych wektorów:
KL→=L−K=[2−(−1), 5−1]=[3, 4]
KM→=M−K=[−2−(−1), 3−1]=[−1, 2]
Liczysz teraz wyznacznik tych wektorów (patrz: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 )
d(KL→, KM→)=
| 3 4 |
| −1 2 |
=3*2−4*(−1)=6+4=10
 W trójkącie KLM K=(−1;1), L =(2;5), M=(−2;3)
d) napisz równanie środkowej boku LM
Czy to ma być tak jak na rysunku? Bo jest niejasno sprecyzowane polecenie.
Jeżeli tak, to:
K=(−1; 1)
S=(0; 4)
Liczysz tak jak pkt. a) − prosta przechodząca przez 2 punkty K i S.
W trójkącie KLM K=(−1;1), L =(2;5), M=(−2;3)
d) napisz równanie środkowej boku LM
Czy to ma być tak jak na rysunku? Bo jest niejasno sprecyzowane polecenie.
Jeżeli tak, to:
K=(−1; 1)
S=(0; 4)
Liczysz tak jak pkt. a) − prosta przechodząca przez 2 punkty K i S.

 i równanie prostych prostopadłych też !
Koniec tematu
i równanie prostych prostopadłych też !
Koniec tematu 
 ! A nie każdy na to wpadnie, jak w poleceniu tego nie ma. Podałem
wektorową metodę obliczania pola, bo jest uniwersalna i prosta i pasuje do każdego przypadku.
! A nie każdy na to wpadnie, jak w poleceniu tego nie ma. Podałem
wektorową metodę obliczania pola, bo jest uniwersalna i prosta i pasuje do każdego przypadku.
 Miłych snów
Miłych snów



 !
Nie zniewalaj, nie narzucaj ! ucz uczniów logicznego myślenia!
Przeczytaj uważnie co napisała Aga!
!
Nie zniewalaj, nie narzucaj ! ucz uczniów logicznego myślenia!
Przeczytaj uważnie co napisała Aga!


 ? A jeżeli chcesz wiedzieć, mam doświadczenie z
uczniami nie mniejsze niż Ty i wiem, jakie metody lepiej rozumieją, a na pewno krótkie i
przejrzyste metody, których ich uczę, wchodzą im do głowy lepiej niż szkolne tasiemcowe wzory
długie na dwie linijki czy uwielbiane przez nauczycieli układy równań z milionem niewiadomych
stosowane tam, gdzie z powodzeniem wystarczy równanie z jedną niewiadomą. Pozdrawiam Cię i
lepiej będzie jezeli zajmiemy się oboje pomaganiem innym, którzy tej pomocy od nas oczekują.
? A jeżeli chcesz wiedzieć, mam doświadczenie z
uczniami nie mniejsze niż Ty i wiem, jakie metody lepiej rozumieją, a na pewno krótkie i
przejrzyste metody, których ich uczę, wchodzą im do głowy lepiej niż szkolne tasiemcowe wzory
długie na dwie linijki czy uwielbiane przez nauczycieli układy równań z milionem niewiadomych
stosowane tam, gdzie z powodzeniem wystarczy równanie z jedną niewiadomą. Pozdrawiam Cię i
lepiej będzie jezeli zajmiemy się oboje pomaganiem innym, którzy tej pomocy od nas oczekują.

 ! Pokazuję zawsze, skąd wzięły się krótsze metody. Poza tym
co widzisz złego w nauczaniu prostszych metod? Dzięki temu uczniowie znają krótsze i logiczne
sposoby, zadania zajmują im mniej czasu, rozwiązując krótszym, przejrzystym i obrazowym
sposobem robią mniej błędów, a to zwiększa ich szanse na zdanie matury, bo na maturze niestety
liczy się czas. Uczeń znający krótkie metody zrobi dajmy na to trzy zadania, podczas gdy uczeń
"wyedukowany" (celowo w cudzysłowiu) topornymi i długimi szkolnym metodami w tym samym czasie
zrobi jedno zadanie, bo np. będzie przepisywał 20 razy równanie rozwiązując układ równań, mimo
że nie jest to potrzebne, będzie rozwiązywał zadanie z rzutu trzema kostkami drzewkiem i
rysował krzaka na całą kartkę A4, zamiast zastosować np. regułę mnożenia, będzie obliczał pole
trójkąta obliczając po kolei wszystkie odcinki, zamiast zrobić to wyznacznikiem wektorów i
ledwo wyciągnie, jak mu się uda, na te 30 %, bo więcej nie zdąży zrobić. A znając szybkie i
obrazowe metody ten sam uczeń zda maturę dajmy na to na 50 % i będzie lepiej rozumiał
zagadnienia.
Wiem, co u mnie zrobiono na prawdopodobieństwie w LO. Posadzono im te krzaki chyba korzeniem na
głębokości co najmniej 5 m pod ziemią, ja daję potem uczniowi zadanie z rzutem trzema
monetami, a on mi zaczyna dżunglę amazońską malować, zamiast zrobic to reguła mnożenia, co
zajęłoby mu 3 linijki i 2 minuty. I jak tu mówić o edukacji
! Pokazuję zawsze, skąd wzięły się krótsze metody. Poza tym
co widzisz złego w nauczaniu prostszych metod? Dzięki temu uczniowie znają krótsze i logiczne
sposoby, zadania zajmują im mniej czasu, rozwiązując krótszym, przejrzystym i obrazowym
sposobem robią mniej błędów, a to zwiększa ich szanse na zdanie matury, bo na maturze niestety
liczy się czas. Uczeń znający krótkie metody zrobi dajmy na to trzy zadania, podczas gdy uczeń
"wyedukowany" (celowo w cudzysłowiu) topornymi i długimi szkolnym metodami w tym samym czasie
zrobi jedno zadanie, bo np. będzie przepisywał 20 razy równanie rozwiązując układ równań, mimo
że nie jest to potrzebne, będzie rozwiązywał zadanie z rzutu trzema kostkami drzewkiem i
rysował krzaka na całą kartkę A4, zamiast zastosować np. regułę mnożenia, będzie obliczał pole
trójkąta obliczając po kolei wszystkie odcinki, zamiast zrobić to wyznacznikiem wektorów i
ledwo wyciągnie, jak mu się uda, na te 30 %, bo więcej nie zdąży zrobić. A znając szybkie i
obrazowe metody ten sam uczeń zda maturę dajmy na to na 50 % i będzie lepiej rozumiał
zagadnienia.
Wiem, co u mnie zrobiono na prawdopodobieństwie w LO. Posadzono im te krzaki chyba korzeniem na
głębokości co najmniej 5 m pod ziemią, ja daję potem uczniowi zadanie z rzutem trzema
monetami, a on mi zaczyna dżunglę amazońską malować, zamiast zrobic to reguła mnożenia, co
zajęłoby mu 3 linijki i 2 minuty. I jak tu mówić o edukacji ? Drzewka to naprawdę świetna
metoda, ale do zadań z prawdopodobieństwa całkowitego, bez sensu jest stosować ją tam, gdzie
można wykonać proste obliczenia kombinatoryczne. Pozdrawiam.
? Drzewka to naprawdę świetna
metoda, ale do zadań z prawdopodobieństwa całkowitego, bez sensu jest stosować ją tam, gdzie
można wykonać proste obliczenia kombinatoryczne. Pozdrawiam.