Funkcja liniowa z parametrem
LaBruja:
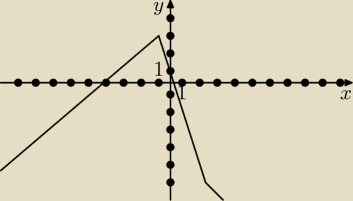
Naszkicuj wykres funkcji f(x)=
√4−4x+x2−2
√x2+2x+1. Korzystając z wykresu funkcji f
określ liczbę rozwiązan równania f(x)=−2x+b w zależności od wartości parametru b.
Proszę o rozwiązanie i wytłumaczenie, bo w ogóle nie rozumiem zadań z parametrem.
f(x)=
√4−4x+x2−2
√x2+2x+1=|x−2|−2|x+1|
| | ⎧ | x+4 dla x∊(−∞,−1) | |
| f(x)= | ⎨ | −3x dla x∊<−1; 2) |
|
| | ⎩ | −x−4 dla x∊<2; +∞) | |
7 gru 22:17
agniecha: rysunek jest źle
7 gru 22:27
LaBruja: dlaczego?
7 gru 22:56
LaBruja: jeżeli chodzi o miejsca zerowe to jak rysowałam to mi się pokrywały...
x0=−4 v x0=0
ten czubek u gór ma współrzędne (−1;3), a na dole (2;−6)
7 gru 23:01
Aga: Wykres przechodzi przez punkt (0,0).
8 gru 07:32
LaBruja: No to napisałam miejsce zerowe x0=0.
Czy ktoś pomoże mi rozwiązać i wytłumaczy mi co robić z dalej?
8 gru 10:39
aa: napisałaś układ równań więc dal każdego warunku stwórz osobną tabelkę pamiętając że x∊ ....
8 gru 10:52
LaBruja: Jaką tabelę? Kompletnie nie mam pojęcia co robić! Jak mam określić liczbę rozwiązań równania
f(x)=−2x+b w zależności od wartości parametru b? wiem, że jak by było np. f(x)=m to patrzymy
liniami równoległymi do osi OX... ale tego już w ogóle nie łapię

8 gru 11:13
aa: x+4 dla x∊(−∞, −1)
x | ....|−4 | −3 | −2
y |.....| 0 | 1 | 2
−3x dla x∊<−1, 2)
x | −1 | 0 |1
y | 3 | 0| −3
−x−4 dla x∊<2, +∞)
x | 2 | 3 | 4 ....
y | −6|−7|−8 ...
i teraz narysuj swoje f(x)
8 gru 11:28
LaBruja: No i co z tym parametrem?
8 gru 11:34
lula :
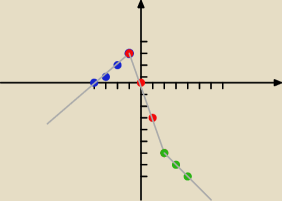
8 gru 11:38
LaBruja: I skąd mam wiedzieć ile rozwiązań dla jakiej wartości parametru b?
8 gru 11:40
lula : y=−2x+b
co się dzieje gdy b=0 ile jest rozwiązań − narysuj taką prostą
co się dzieje z narysowaną prostą gdy b>0 a wtedy ile jest rozwiązań
co się dzieje z narysowaną prostą gdy b<0 a wtedy ile jest ..... ?
8 gru 11:52
LaBruja: Dzięki chyba teraz rozumiem!

ile jest punktow przecięcia tyle rozwiązań
czyli dla b∊(−
∞5;1)\{−5} 2 rozwiązania, b∊{1} 1 rozwiąnie, b∊(1;+
∞) nie ma rozwiązań, b∊{−5}
nieskończenie wiele rozwiązań
tylko w odpowiedziachjest inaczej

8 gru 12:15
lula : nieee
a jak jest w odpowiedziach
8 gru 12:25
LaBruja: (−2;1) 3 rozwiązania
{−2;1} 2 rozwiążania
(−
∞;−2)∪(1,+
∞) 1 rozwiązanie
aha już wiem spieprzyłam rysując prostą i wychodziła zawsze równoległa do wykresu w ostatnim
przedziale... ale teraz juz powinno mi wyjść, dzięki wszystkim

mam tylko pytanie: zawsze jak mamy takie zadanie z parametrem to musimy rysować wykres tej
funkcji z parametrem, a pozniej sprawdzac dla jakich jego wartosci, co i jak, czy jest jakiś
inny sposób?
8 gru 12:39
lula : to jest najłatwiejszy i najszybszy
8 gru 12:50
LaBruja: Dzięki

8 gru 12:59
 Naszkicuj wykres funkcji f(x)=√4−4x+x2−2√x2+2x+1. Korzystając z wykresu funkcji f
określ liczbę rozwiązan równania f(x)=−2x+b w zależności od wartości parametru b.
Proszę o rozwiązanie i wytłumaczenie, bo w ogóle nie rozumiem zadań z parametrem.
f(x)=√4−4x+x2−2√x2+2x+1=|x−2|−2|x+1|
Naszkicuj wykres funkcji f(x)=√4−4x+x2−2√x2+2x+1. Korzystając z wykresu funkcji f
określ liczbę rozwiązan równania f(x)=−2x+b w zależności od wartości parametru b.
Proszę o rozwiązanie i wytłumaczenie, bo w ogóle nie rozumiem zadań z parametrem.
f(x)=√4−4x+x2−2√x2+2x+1=|x−2|−2|x+1|


 ile jest punktow przecięcia tyle rozwiązań
czyli dla b∊(−∞5;1)\{−5} 2 rozwiązania, b∊{1} 1 rozwiąnie, b∊(1;+∞) nie ma rozwiązań, b∊{−5}
nieskończenie wiele rozwiązań
tylko w odpowiedziachjest inaczej
ile jest punktow przecięcia tyle rozwiązań
czyli dla b∊(−∞5;1)\{−5} 2 rozwiązania, b∊{1} 1 rozwiąnie, b∊(1;+∞) nie ma rozwiązań, b∊{−5}
nieskończenie wiele rozwiązań
tylko w odpowiedziachjest inaczej 
 mam tylko pytanie: zawsze jak mamy takie zadanie z parametrem to musimy rysować wykres tej
funkcji z parametrem, a pozniej sprawdzac dla jakich jego wartosci, co i jak, czy jest jakiś
inny sposób?
mam tylko pytanie: zawsze jak mamy takie zadanie z parametrem to musimy rysować wykres tej
funkcji z parametrem, a pozniej sprawdzac dla jakich jego wartosci, co i jak, czy jest jakiś
inny sposób?
