Układy równań
Marlenka: Rozwiązać następujące układy równań i podać ich interpretacje geometryczną:
O co chodzi z tą interpretacją geometryczną? I jakim sposobem rozwiązywać te układy równań
gdzie jest np. x
2.
6 gru 16:06
Marlenka: Proszę o pomoc, przynajmniej o wytłumaczenie tego.
6 gru 17:10
Patryk: interpretacja geometryczna to narysowanie tych funkcji
6 gru 17:12
Marlenka: W układzie współrzędnych czy tylko na osi?
6 gru 17:16
Patryk: w układzie
6 gru 17:16
Patryk: rysujesz dwie funkcje i patrzysz gdzie maja punkt przecięcia
6 gru 17:17
Marlenka: Ok, a może orientujesz się jak rozwiązać np. b?
6 gru 17:18
Marlenka: Czyli mogę narysować tabelkę z trzema liczbami i tak narysować te funkcje, czy mam korzystać z
wyników?
6 gru 17:19
Patryk: ok spróbuje napisać , a czy ty znasz jakaś metodę rozwiązywania układów równań ?
6 gru 17:19
Patryk: jak rysujesz funkcje to normalnie z tabelki
6 gru 17:21
Marlenka: Tak, Metode przeciwnych współczynników i metoda podstawiania.
6 gru 17:22
Patryk: a) mozna zrobic tymi 2 metodami
6 gru 17:24
Marlenka: tak, podpunkt a potrafię rozwiązać, ale kompletnie nie wiem jak będzie z tym "b" tam gdzie jest
mnożenie i x z y są do kwadratu.
6 gru 17:27
Patryk: a masz wyniki do tego b) ? wychodzą mi dziwne wyniki
6 gru 17:31
Marlenka: Nie, nie mam żadnych odpowiedzi do zadań.
6 gru 17:33
Patryk: w c)
x
2+x=4
x
2+x−4=0 < to znasz ?
6 gru 17:47
Basia: funkcja kwadratowa i mam liczyć delte?
6 gru 17:49
Patryk: tak, jest żle ?
6 gru 17:50
Marlenka: Czyli mam liczyć tą delte?
6 gru 17:50
Marlenka: Spróbuje to jakoś policzyć przez tą delte, dziękuje za pomoc

6 gru 17:51
Patryk: tak
6 gru 17:51
Patryk: c) x2−2x=y
d) ⎩ −x2+4x=y
−x
2+4x=x
2−2x
−x
2+4x−x
2+2x=0
−2x
2+6x=0
−2x
2+6x=0/ *(−1)
2x
2−6x=0
x(2x−6)=0
x=0 2x−6=0⇒ 2x=6
x=3
6 gru 17:58
Marlenka: ok, dzięki za rozwiązanie tego ostatniego
6 gru 18:12
Patryk: te x sy jeszcze trzeba wstawić do któregoś z równania i otrzymać y
6 gru 18:15
Marlenka: tak wiem, teraz zastanawiam się nad tym b, bo raczej tego met. podstawiania nie da się zrobić
6 gru 18:21
Patryk: mogę ci to rozpisać, jak to zacząlem robić wychodzi równanie typu a4+b2+c=0 z dziwnymi
wynikami
,zaraz napisze ,ale było by dobrze gdyby mnie ktoś z forum tez sprawił
6 gru 18:25
Patryk:
1+y
4=4y
2
1+y
4−4y
2=0
y
4−4y
2+1=0
6 gru 18:30
Patryk: to co napisalem to metoda podst.
6 gru 18:31
6 gru 18:32
Marlenka: chyba,że
y4−4y2+1=0
x2(y2−4)+1=0
x2=0
y2=3
6 gru 18:33
Patryk: co do czego wstawiłaś bo nie wiem skąd to x2
6 gru 18:36
Marlenka: pomyłka to miał być y2 wyciągnięty z nawiasu
6 gru 18:37
6 gru 18:40
Aga:
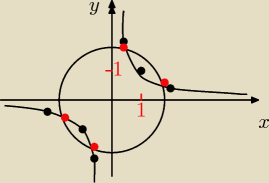
b) interpretacja geometryczna
x
2+y
2=4→okrąg S(0,0), r=2
xy=1//:x ,x≠0
Jak widać układ ma 4 rozwiązania (punkty przecięcia okręgu z hiperbolą.)
6 gru 18:42
Marlenka: A "c" tam będzie parabola czyli też będzie więcej niż 2 rozwiązania?
6 gru 18:48
Marlenka: c) x2+x=4
x2+x−4=0
Δ= 1+16=17
√Δ=√17
6 gru 18:58
Aga:
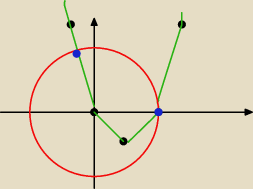
c)
6 gru 19:04
Marlenka: ok, ale jak to zapisać?
6 gru 19:06
Aga: Fatalnie, jedno równanie wzięłam z c, a drugie z d.
6 gru 19:15
Aga:
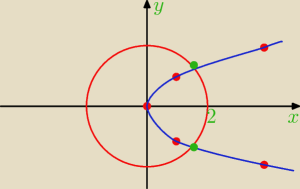
c)x=y
2
x
2+y
2=4
6 gru 19:19
Marlenka: A jak mam to rozwiązać?
6 gru 19:35
Aga: x=y2, x≥0
x2+y2=4
x2+x−4=0
Δ=17
6 gru 19:40
Marlenka: ok, bardzo dziękuje za pomoc

6 gru 19:44

 b) interpretacja geometryczna
x2+y2=4→okrąg S(0,0), r=2
xy=1//:x ,x≠0
b) interpretacja geometryczna
x2+y2=4→okrąg S(0,0), r=2
xy=1//:x ,x≠0
 c)
c)
 c)x=y2
x2+y2=4
c)x=y2
x2+y2=4
