stereometria Matma: Parę zadań ze stereometrii, których nie jestem w stanie zrobić, a ich bardzo potrzebuję. 1 Dany jest ostrosłup prawidłowy czworokątny, którego objętość jest równa 18. Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 4. Oblicz wysokość tego o ostrosłupa. 2 Dany jest ostrosłup prawidłowy czworokątny o długości każdej krawędzi a = 8. Wyznacz objętość tego ostrosłupa. 3 W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstaw pod kątem o mierze 60 stopni. Wysokość ściany bocznej ma długość 8. Wyznacz długość krawędzi podstawy ostrosłupa. 4 Dany jest ostrosłup prawidłowy czworokątny o wszystkich krawędziach jednakowej długości, na którego podstawie opisano okrąg o promieniu 2√2. Wyznacz objętość. 5 Dany jest ostrosłup prawidłowy trójkątny, w którego podstawę wpisano w okrąg o promieniu 2√3. ściany boczne są trójkątami równobocznymi. Wyznacz objętość.

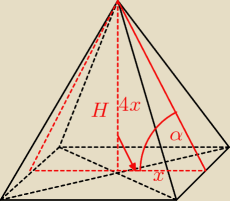
Gustlik: Zad. 1. V=18, tgα=4 W zadaniach, gdzie masz dane takie wielkości, które zazwyczaj się oblicza, jak np. pole czy objetość, stosuj zawsze zasade "co masz dane, to obliczasz, a potem przyrównujesz". Czyli jeżeli dane jest pole − obliczasz to pole, a jak objetośc − obliczasz objetość, wstawiając w miejsce nieznanych danych niewiadome. Tak obliczone pole/objetość przyrównujesz do wartości podanej w zadaniu i równaniem obliczasz te niewiadome. Mam daną objetość, więc ją obliczam, a potem przyrównam do podanej w zadaniu:

	1
V=		PpH
	3

P_p=(2x)²=4x² H=4x

	1		16
V=		*4x2*4x=		x3
	3		3

16
	x3=18 /*3
3

16x³=54 /:16

	54		27
x3=		=		/3√
	16		8

	3
x=
	2

	3
H=4x=4*		=2*3=6
	2

Odp. H=6

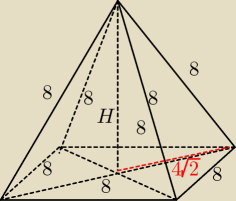
Gustlik: Zad. 2.Dany jest ostrosłup prawidłowy czworokątny o długości każdej krawędzi a = 8. Wyznacz objętość tego ostrosłupa.

	1
V=		PpH
	3

P_p=8²=64 H²+(4√2)²=8² H²+32=64 H²=64−32=32 /√ H=√32=4√2

	1
V=		*64*4√2
	3

	256√2
V=
	3