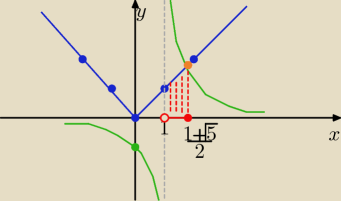
helpunio JULIA: POMOCY. funkcje ŁATWE Dane są funkcje F(x) = |x| oraz g(x) = 1/(x−1). Wyznacz te argumenty x, dla których funkcja (f) osiąga wartości mniejsze niż funkcja g

morfepl: skoro łatwe, to czemu nie zrobisz?

JULIA: bo dla was to jest tylko łatwe ;C

JULIA: uwierz mi ze wlozylam duzy wklad zeby to zrobic , i skonczylam na narysowaniu funkcji dalej nie umiem obliczyc

tomasz: 1/(x−1)>|x|

ZKS: f(x) < g(x)

	1
|x| <
	x − 1

(|x|(x − 1) − 1)(x − 1) < 0 Dla x ≥ 0 (x² − x − 1)(x − 1) < 0

	1 − √5		1 + √5
(x −		)(x −		)(x − 1) < 0
	2		2

	1 − √5		1 + √5		1 + √5
x ∊ (−∞ ;		) ∪ (1 ;		) ∧ x ≥ 0 ⇒ x ∊ (1 ;		)
	2		2		2

Dla x < 0 (−x² + x − 1)(x − 1) < 0 x > 1 ∧ x < 0 ⇒ x ∊ ∅ Ostatecznie:

	1 + √5
x ∊ (1 ;		)
	2

tomasz: jeśli dalej nie wiesz, to 1/(x−1) − |x| > 0 dla x ≥ 0 1/(x−1) − x > 0 1/(x−1) − x(x−1)/(x−1) > 0 1−x(x−1)/(x−1) > 0 dla x<0 1/(x−1) +(x−1)/(x−1)>0 1+x(x−1)/(x−1)>0

Eta: