rumpek:
f(x) =−2x
2 − 3x + 2
1
o Punkt przecięcia z Ox − po prostu szukasz miejsc zerowych wtedy będzie przecinało oś
odciętych
−2x
2 − 3x + 2 = 0
Δ = 9 + 2*2*4 = 9 + 16 = 25 ⇒
√Δ = 5
2
o Z osią rzędnych Oy przecina się tylko gdy x = 0, więc podstawiamy
y = −2(0)
2 − 3*0 + 2
y = 2
3
o Zbiór wartości to druga współrzędna wierzchołka W(x
w, y
w)
| | Δ | | 25 | | 25 | |
yw = − |
| = − |
| = |
| |
| | 4a | | −8 | | 8 | |
Widzimy, że współczynnik a funkcji jest a < 0 więc funkcja malejąca (ramiona w dół) więc zbiór
| | 25 | |
wartości funkcji to będzie: Zw∊(−∞; |
| > |
| | 8 | |
4
o Przedziały monotoniczności to po prostu trzeba znaleźć pierwszą współrzędną wierzchołka
W(x
w, y
w)
Możesz sobie dla ułatwienia narysować tę funkcję, lecz widać, że:
| | 3 | |
− funkcja jest rosnąca dla x∊(−∞; − |
| > |
| | 4 | |
| | 3 | |
− funkcja jest malejąca dla x∊<− |
| ; +∞) |
| | 4 | |

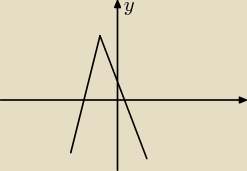 jezeli parabola przecina os y to ile wynosi x w miejscu przeciecia?
jezeli parabola przecina os y to ile wynosi x w miejscu przeciecia?




