funkcja ddd: miejscem zerowym funkcji f jest x=−2 .wyznacz równanie prostej bedącej wykresem funkcji ,jesli jest ona prostopadła do prostej −3/4x−9/8y+3=0

Eta: Przekształcamy równanie prostej do postaci kierunkowej

	3		9
−		x−		y+3=0 /*(−8)
	4		8

9y= −6x+24

	2		24		2
y= −		x+		a1= −
	3		9		3

	3
współczynnik kierunkowy prostej prostopadłej : a2=
	2

f(x)= ax+b f(−2)=0 to 0= −2a+b => b= 2a

	3		3
f(x)=		x+2*
	2		2

	3
f(x)=		x+3
	2

ddd: kto pomoże ? dana jest funkcja f(x)=−2x²−3x+2 −wyznacz współrzędne punktów przecięcia wykresu tej funkcji z osiami układu współrzędnych. −podaj zbiór wartości oraz przedziały monotoniczności POMOCY

ddd: dziękuję ETA za pomoc

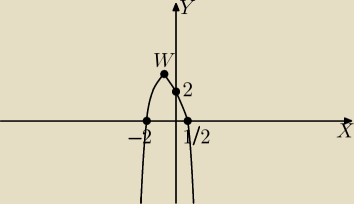
Gustlik: f(x)=−2x²−3x+2 Δ=b²−4ac=9−4*(−2)*2=9+16=25, √Δ=5

	−b−√Δ		3−5		1
x1=		=		=
	2a		−4		2

	−b+√Δ		3+5
x2=		=		=−2
	2a		−4

	1
Punkty przecięcia z osią OX: (		, 0) i (−2, 0) − są to miejsca zerowe.
	2

Punkt przecięcia z osią OY: (0, c)=(0, 2).

	−b		3
p=		=−
	2a		4

	−Δ		25		1
q=		=		=3
	4a		8		8

	3		1
Wierzchołek paraboli W=(−		, 3		)
	4		8

	1
Zbiór wartości ZW=(−∞, 3		>
	8

	3
Monotoniczność: f(x)↗ dla x∊(−∞, −		>
	4

	3
f(x)↘ dla x∊(−		, +∞>
	4

Gustlik: Mały chochlik w ostatnim wierszu − domknięcie przedziałów:

	3
Powinno być tak: f(x)↘ dla x∊<−		, +∞). To nieraz tak się dzieje, jak się robi
	4

kopiuj−wklej i nie zauważy wszystkiego, co trzeba zmienić. Pozdrawiam

fff: √81