pole trójkąta Monika: na konkursie z matematyki spotkałam się z zadaniem: Oblicz pole trójkąta, którego dwa boki maja długości 3 i 5, a środkowa poprowadzona do trzeciego boku ma długość 2. Czy jest możliwość wytłumaczenia mi tego zadania?

M:

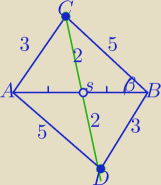
Mila: 1) Przedłużamy środkową jak na rysunku 2)ACBD jest równoległobokiem ( przekątne dzielą się na połowy) 3) |AB|²+4²==2*5²+2*3² |AB|²=50+18−16 |AB|²=52 |AB|=2√13 4) Pole można obliczyć np. tak: a) z wzoru Herona ( wbrew obawom, że: |AB|=2√13 ) p=4+√13 P_Δ=√(4+√13)*(4+√13−2√13)*(4+√13−3)*(4+√13−5) P_Δ=√(4+√13)*(4−√13)*(√13+1)*(√13−1) P_Δ=√3*12=6 lub b) Z tw. cosinusów obliczymy cosinus kąta ACB

	3
cos C=−		− kąt C z II ćwiartki
	5

	4
sinC=
	5

P_Δ=6 =================

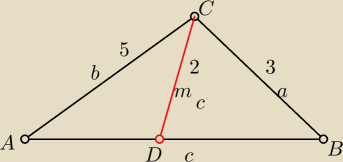Lao Mao: m_c− dlugośc srodkowej poprowadzonej z wierzchołka C m_c=2 a=3 b=5 i c>0

	√2(a2+b2)−c2
mc=
	2

2m_c=√2(a²+b²)−c² 4=√2(3²+5²)−c² /² 16=2(9+25)−c² −52=−c² c²=52 c=√52=2√13 Dalej jak u Mili

Mila:

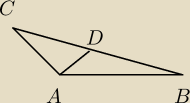Leszek: |AB|=5 , |AC|=3 , |AD|=2, ∡ADC =α , |CD|= |DB} = x P_ΔABD = P_ΔADC= 0,5dxsinα , P_ΔABC = dxsinα z tw.cosinusow: dla ΔADC ; 9= x²+4 −4xcosα , ⇒x² −4cosα =5 dla ΔABD : 25 = x² +4 + 4cosα ⇒x² +4cosα = 21 z tych dwoch rownan ⇒x = √13 zatem : 13 −4√13cosα = 5⇒cosα = 2√13/13⇒ sinα = 3√13/13 czyli P_ΔABC = 6