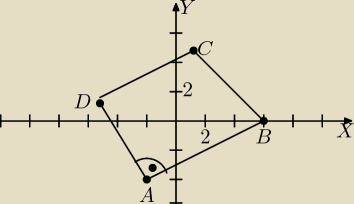
Oblicz współrzędne wierzchołka D tego trapezu dul: Znane są wierzchołki A=(−2,−4), B=(6,0), C=(1,5) trapezu prostokątnego o podstawach AB i CD. Oblicz współrzędne wierzchołka D tego trapezu

Basia: ponieważ BC^→=[−5;5] nie jest prostopadły do AB^→[8,4] to AD^→ musi być prostopadły do AB^→ i wobec tego: 1. napisz równanie pr.AB 2. napisz równanie pr.AD⊥pr.AB i przechodzącej przez A 3. napisz równanie pr.CD || pr.AB i przechodzącej przez C 4. rozwiąż układ równań pr.AD i pr.CD jego rozwiązanie to współrzędne D

Gustlik: Znane są wierzchołki A=(−2,−4), B=(6,0), C=(1,5) trapezu prostokątnego o podstawach AB i CD. Oblicz współrzędne wierzchołka D tego trapezu Badam prostopadłość wektorów BC^→=[−5;5] i AB^→[8,4] (skorzystałem z obliczeń Basi) Iloczyn skalarny BC^→*AB^→=−5*8+5*4=−40+20=−20≠0, więc wektory nie są prostopadłe. Zatem wektorem prostopadłym do AB^→ bedzie AD^→. Liczę współczynnik kierunkowy pr. CD jako prostej równoległej do wektora AB^→=[8, 4]

	wy
a=		, gdzie [wx, wy] − wspołrzędne wektora równoległego do prostej.
	wx

	1
a1=U[4}{8}=
	2

	1
Pr. CD∥: y=		x+b
	2

Wstawiam wsp. C=(1, 5)

	1
5=		*1+b
	2

	1
4		=b
	2

	1
b=4
	2

	1		1
Pr. AB: y=		x+4
	2		2

	1
Zatem wspólczynnik kierunkowy pr. AD a2=−		=−2 (war. prostopadłości).
	a1

Pr. AD: y=−2x+b, A=(−2, −4) −4=−2*(−2)+b −4=4+b b=−8 y=−2x−8

	1		1
{y=		x+4
	2		2

{y=−2x−8

1		1
	x+4		=−2x−8 /*2
2		2

x+9=−4x−16 5x=−25 /:5 x=−5 y=−2*(−5)−8 y=10−8 y=2 Odp: D=(−5, 2) x=−2

Gustlik: To x=−2 w ostatniej linijce to chochlik − nie brać tego pod uwagę.