Nierówność z wartością bezwzględną
Hubert: Witam mam takie oto równanie:
4|x|−|x|3 ≤ 0
mam je rozwiązać i robię to metodą podstawników jednak w późniejszym etapie źle mi wychodzi
"wężyk". Proszę o pomoc jak to rozwiązać!
sam zrobiłem w ten sposób:
4|x|−|x|3 ≤ 0
|x|(4−|x|2)≤0 |x|=d d≥0
d(4−d2)≤0
d=0 d=2 d=−2
Co robię źle ?
4 gru 17:29
Aga: IxI2=x2
IxI(2−x)(2+x)≤0
rozpatrujesz dwa przypadki
Dla x≥0
x(2−x)(2+x)≤0
Dla x<0
−x(2−x)(2+x)≤0
4 gru 17:32
Basia:
wszystko jest dobrze tylko zadanie nie jest skończone
0, −2, 2 to miejsca zerowe
teraz rozwiąż nierówność
d(d−2)(d+2) ≤ 0
fala, wykres, rachunkowo − jak wolisz
i wróć do x
4 gru 17:33
Hubert: No dobra Basiu, ale jak już ma mte miejsca zerowe zaznaczone na osi x (−2,0,2) to jak mam
narysowac ten wezyk? Wg podrecznika fala powinna odbijac sie tylko od podwojnych pierwiastkow
wielomianu. A w odpowiedziach jest zaznaczony przedzial x∊(−niesk. ; −2)suma(0)suma(2;+niesk).
A mi wychodzi ze zero jest pierwiastkiem jednokrotnym wiec nie rozumiem dlaczego w
odpowiedziach jest tak napisane

4 gru 17:42
Hubert: ponawiam prosbe jeszcze raz zeby ktos mi wytlumaczyl najlepiej krok po kroku...
4 gru 19:06
Basia:
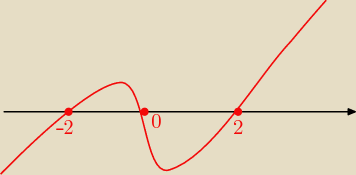
d(d−2)(d+2) zmienia znak w punktach −2, 0 , 2
zaczynasz od (−)
czyli:
d∊(−
∞;−2>∪<0;2>
i rozwiązujesz:
|x| ≤ −2 (niemożliwe)
lub
|x|≥ 0 (zawsze prawdziwe) i |x|≤2
czyli zostaje tylko
|x|≤2 ⇔ x∊<−2;2>
4 gru 19:20
florian: odpowiedz do zadania niestety jest inna : x∊(−
∞;−2>∪(0)∪<2;
∞> więc nadal cos musi być źle w tym
rozwiązaniu... Ponadto nie ma (d−2)(d+2) tylko conajwyżej (2−d)(2+d)

4 gru 19:31

 d(d−2)(d+2) zmienia znak w punktach −2, 0 , 2
zaczynasz od (−)
czyli:
d∊(−∞;−2>∪<0;2>
i rozwiązujesz:
|x| ≤ −2 (niemożliwe)
lub
|x|≥ 0 (zawsze prawdziwe) i |x|≤2
czyli zostaje tylko
|x|≤2 ⇔ x∊<−2;2>
d(d−2)(d+2) zmienia znak w punktach −2, 0 , 2
zaczynasz od (−)
czyli:
d∊(−∞;−2>∪<0;2>
i rozwiązujesz:
|x| ≤ −2 (niemożliwe)
lub
|x|≥ 0 (zawsze prawdziwe) i |x|≤2
czyli zostaje tylko
|x|≤2 ⇔ x∊<−2;2>
