Wymierna
Karlo: Siemanko.
Dla jakich wartości m równanie ma rozw. dodatnie
9x −5mx −3m +20, nie bardzo wiem co robić, pomożecie?

4 gru 16:13
Karlo: a więc..?

4 gru 16:42
Bogdan:
a gdzie jest to równanie?
4 gru 16:45
Karlo: to było wymierne tylko wymnożyłem
9x −5mx −3m +20 =0
4 gru 16:46
4 gru 16:48
Ines: i teraz oblicz deltę i narysuj
4 gru 16:48
Karlo: jaką delte...?
4 gru 16:49
Karlo: mam to odjac i do wspólnego...?
4 gru 16:50
Ines: | 5(mx−4)−3(3x−m) | |
| |
| (3x−m)(mx−4) | |
4 gru 16:53
Karlo: i dół większy od zera?
4 gru 16:55
Bogdan:
| | m | | 4 | |
Założenie: x ≠ |
| i x ≠ |
| |
| | 3 | | m | |
| | 20 − 3m | | 9 | |
5mx − 20 = 9x − 3m ⇒ (5m − 9)x = 20 − 3m ⇒ x = |
| , m ≠ |
| |
| | 5m − 9 | | 5 | |
| | 20 − 3m | |
x > 0 ⇒ |
| > 0 ..... |
| | 5m − 9 | |
Rozwiąż ostatnią nierówność.
4 gru 16:55
Ines: oblicz to
| 5(mx−4)−3(3x−m) | |
| =0 |
| (3x−m)(mx−4) | |
i następnie
[ 5(mx−4)−3(3x−m) ] * [ (3x−m)(mx−4) ] = 0 i zaznacz na osi zbiór rozwiązań najlepiej metodą
węzyka i odczytaj rozwiązanie

4 gru 16:55
Ines: + założenia
4 gru 16:56
Bogdan:
Ines − nie mieszaj
4 gru 16:56
Karlo: dziękuje
4 gru 16:58
Bogdan:
Pokaż Karlo dokończenie zadania
4 gru 16:59
Karlo: ta zaraz będzie

4 gru 17:00
Karlo: wyszło tak?
−15m2 +73m −180>0 ?
4 gru 17:04
Karlo: tzn −15m2 +127m −180>0
4 gru 17:06
Karlo: :Bogdan: jestes pewien że to dobrze jest?
4 gru 17:10
Bogdan:
| | | | 20 | | 9 | |
⇒ |
| > 0 ⇔ −(m − |
| )(m − |
| ) > 0 |
| | | | 3 | | 5 | |
x ∊ .....
dokończ
4 gru 17:10
Bogdan:
nie x ale m ∊ ...
4 gru 17:11
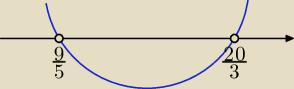
Karlo: (parabola będzie inaczej, do góry zwrócona) , a odp to (9/5, 20/3), z tego co napisałeś
4 gru 17:16
4 gru 17:17
Bogdan:
Widzę, że nie ograniczasz się tylko do przepisywania, ale kontrolujesz zapis rozwiązania.
Oczywiście, że parabola jest skierowana ramionami w dół. Odpowiedź jest taka, jak
podałeś, zgadzasz się z nią?.

4 gru 17:19
Karlo: wszystko wygląda fajnie i dosyć jasno, tylko w odp mam że jeszcze 2√3 nie należy do m
4 gru 17:20
Bogdan:
No coś zrób sam i ustal samodzielnie końcową odpowiedź.
4 gru 17:32
Karlo: | | 9 | | 20 | |
m∊ ( |
| , 2√3) U (2√3 , |
| ) |
| | 5 | | 3 | |
4 gru 17:43





