pomocy
julia: dla mistrza MATEMATYKi. PRAWDOPODOBIENSTWO
W pudełku są trzy rodzaje losów na loterię: jeden los wygrywający, sześć przegrywających i trzy
upoważniające do ponowenego lodowania. Możemy kupić tylko jeden los.
A − jakie jest prawd., że wygramy?
3 gru 20:17
Eta:
Hehe

tu nie potrzeba "mistrza" ( wystarczy logicznie pomyśleć)
R−m : 10 losów
A −−− wygrana
| | 1 | |
1/ wylosujemy los wygrywający i mamy P(A1) = |
| −−− wygrana za pierwszym razem |
| | 10 | |
| | 3 | |
2/ wylosujemy los upoważniający do ponownego losowania z prawdopodobieństwem |
| |
| | 10 | |
A
2 −−− wylosujemy za drugim razem los wygrywający
| | 3 | | 1 | |
P(A2) = |
| * |
| −−− wygrana za drugim razem |
| | 10 | | 9 | |
A
3 −−− wylosujemy za drugim razem los upoważniający znów do ponownego losowania
| | 3 | | 2 | | 1 | |
i mamy: P(A3)= |
| * |
| * |
| −−− wygrana za trzecim razem |
| | 10 | | 9 | | 8 | |
A
4 −−− za trzecim razem wylosowano znów los upoważniający do ponownego losowania
| | 3 | | 2 | | 1 | | 1 | |
P(A4)= |
| * |
| * |
| * |
| −−− wygrana |
| | 10 | | 9 | | 8 | | 7 | |
zatem P(A)= P(A
1)+P(A
2)+P(A
3) + P(A
4)=......... dokończ obliczenia
3 gru 20:51
Gustlik:
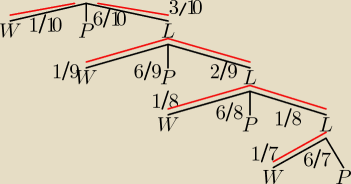
Oznaczenia:
W − wygrana
P − przegrana
L − ponowne losowanie
| | 1 | | 3 | | 1 | | 3 | | 2 | | 1 | | 3 | | 2 | | 1 | | 1 | |
P(W)= |
| + |
| * |
| + |
| * |
| * |
| + |
| * |
| * |
| * |
| =... |
| | 10 | | 10 | | 9 | | 10 | | 9 | | 8 | | 10 | | 9 | | 8 | | 7 | |
dokończ.
3 gru 23:07
Eta:
Znów te "krzaki"

3 gru 23:08
Gustlik: @P[Eta]], sama dobrze wiesz, że nie jestem zwolennikiem krzaków, zwłaszcza tam, gdzie można
zastąpić je kombinatoryką, ale akurat tutaj akurat dają one obraz. Pozdrawiam

3 gru 23:13
rumpek: krzakoterapia <brrr>
3 gru 23:18
b.: na początku wyciągamy pewną liczbę (od 0 do 3) losów uprawniających do ponownego losowania, aż
w końcu wyciągniemy los przegrywający lub wygrywający. Ponieważ przegrywających jest 6, a
wygrywający 1, to szansa wygranej = 1/7.
3 gru 23:24
Gustlik: @ Do rumpka i Ety
Wiem, mnie też wkurza krzakoterapia stosowana tam, gdzie można użyć prostych obliczeń
kombinatorycznych: reguły mnożenia, n!, permutacji, wariacji czy kombinacji, bo wtedy krzaki
gmatwają te proste zadania. Ale tutaj, gdy jest zadanie podzielone na etapy, które nie da się
rozwiązać jednym wzorem, to krzak daje obraz. Ja też nie lubię krzakoterapii, ale w pewnych
przypadkach (np. prawdopodobieństwo całkowite, doświadczenia wieloetapowe) daje ona obraz.
3 gru 23:40
zporr: b. jesteś najlepszy
4 gru 07:22
 tu nie potrzeba "mistrza" ( wystarczy logicznie pomyśleć)
R−m : 10 losów
A −−− wygrana
tu nie potrzeba "mistrza" ( wystarczy logicznie pomyśleć)
R−m : 10 losów
A −−− wygrana
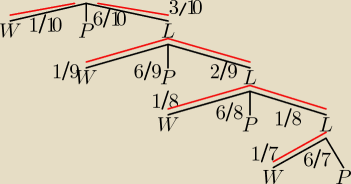 Oznaczenia:
W − wygrana
P − przegrana
L − ponowne losowanie
Oznaczenia:
W − wygrana
P − przegrana
L − ponowne losowanie

