... jeszcze o próbnej maturze
Bizon:
co sądzicie o zadaniu nr z próbnej matury (poziom rozszerzony) i kluczu do jego oceny?
3 gru 17:54
Bizon: zadaniu nr 2 ...
3 gru 17:54
rumpek: Próbnej rozszerzonej z operonu? Ta co była tydzień temu?
Bodajże to zadanie z wykazania że prostokąt jest kwadratem.
Tak to była głupota cała punktacja i całe rozwiązanie.
Skoro udowodniłem, że a = b, a drugi to a + 3 ; b + 3 to też tylko o 3 proporcjonalnie się
zwiększają więc też jest kwadratem. I tak dostałem tylko za to jeden punkt
3 gru 18:04
Bizon:
ktoś długo myślał ... i wymyślił głupawe zadanie ... można mu
... ale klucz do oceny ... to już szczyt głupoty ...
3 gru 18:08
rumpek: zgadzam się 100%
3 gru 18:08
krystek: Bo to jest tak jak ktoś wymyśli i ma "jedyną słuszna rację"
3 gru 18:25
Bizon: jeśli prostokąt o bokach a i b nie jest kwadratem to powiększenie boków o 5 do (a+5) i (b+5)
| | a | | a+5 | |
zmienia proporcję (jeśli a≠b to |
| ≠ |
| )
|
| | b | | b+5 | |
Jak długo trzeba nad tym myśleć aby w kluczu jako prawidłową ścieżkę zakładać
szukanie proporcji między dłuższym bokiem jednego i krótszym drugiego a krótszym pierwszego i
dłuższym drugiego ...
... paranoja
3 gru 18:33
rumpek: Dlatego za 4 pkt zadanie, w kluczu dali punkty za coś oczywistego ...
3 gru 18:55
Bizon: dla mnie to błąd w kluczu
| | a+5 | |
Jeśli a≠b i np a>b ... to mam szukać proporcji |
| ... dłuższego do krótszego  ? |
| | b | |
3 gru 19:29
Bizon:
to urąga podstawom wiedzy o podobieństwie figur
3 gru 19:33
Bogdan:
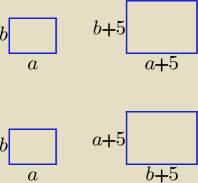
Prostokąt o bokach długości a, b jest podobny do prostokąta o bokach długości a + 5, b + 5.
Wykaż, że te prostokąty są kwadratami.
Nie jest podane w treści zadania, które boki prostokątów są bokami odpowiadającymi sobie.
Trzeba więc rozpatrzeć dwa przypadki:
| | a | | b | |
I przypadek: |
| = |
| |
| | a + 5 | | b + 5 | |
| | a | | b | |
II przypadek: |
| = |
| |
| | b + 5 | | a + 5 | |
3 gru 20:08
Bizon:
jak może powiększenie krótszego boku b o 5 uczynić go bokiem dłuższym od a+5
3 gru 20:19
Bizon: wszak boki ujemnych wartości nie przyjmują
3 gru 20:21
Bogdan:
Nie ma w zadaniu informacji o tym, który bok prostokąta jest dłuższy. Mój rysunek jest
tylko szkicem ilustrującym zagadnienie zawarte w zadaniu, równie dobrze byłoby narysowanie
prostokąta, w którym b > a.
3 gru 20:25
Bizon: ależ to prowadzi do tego samego braku sensu
Jeśli a<b to powiększenie a i b o 5 nie uczyni boku a+5 bokiem dłuższym
3 gru 20:30