oblicz objętość graniastosłupa bv: Mając dany graniastosłup prawidłowy czworokątny, w którym przekątna podstawy równa się a oraz tworzy z przekątną ściany bocznej kąt α ( przekątna podstawy i przekątna ściany bocznej mają wspólny wierzchołek ) oblicz objętość graniast.

bv: Czy ktoś potrafi rozwalić to zadanie?

bv:

rumpek: Pomagam, wpierw rysunek pośle

rumpek: Wspólny wierzchołek to ∡D (na moim rysunku sobie oznaczyłem)

rumpek: Czemu rysunku nie posłało? Dziwne. Jeszcze raz.

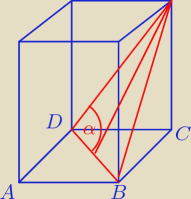
rumpek: Teraz powinno działać

bv: dziękuję − to trochę mi ułatwiło, jednak nie wiem, jak mam z takich danych obliczyć wysokość

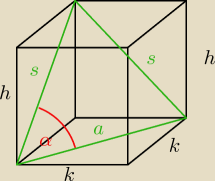
dero2005: s² = s² + a² − 2*a*s*cos α s² − s² − a² + 2a*s*cos α = 0 2a*s*cos α = a²

	a2		a
s =		=
	2a cos α		2cos α

	a√2
k =
	2

	a2		a2		a2−a2cos2α
h = √s2 − k2 = √		−		= √		=
	4cos2α		4		4cos2α

	a2(1−cos2α)		a		sin2α		a
= √		=		√		=		√tg2α =
	4cos2α		2		cos2α		2

	a
=		*tg α
	2

	a√2		a√2		a		a3
V = k*k*h =		*		*		*tg α =		tg α
	2		2		2		4

bv:

	a3√tg2−1
w odp. mam taki wynik:
	4

dero2005: przelicz jeszcze bo może gdziś się pomyliłem w obliczeniach

bv: nie znalazłem błędu

dero2005:

	a2		a2
jest pomyłka, w szóstym wierszu k2 pod pierwiastkiem jest		, powinno być		i
	4		2

wtedy wyjdzie twój wynik

rumpek: Skoro przekątna podstawy to a, zatem bok podstawy ma: x = x√2 (z wiedzy o przekątnej w kwadracie i potem dalsze przekształcenia) a = x√2 / * √2 √2a = 2x / : 2

	a√2
x =
	2

	a√2
Czyli bok podstawy graniastosłupa wynosi: x =
	2

1^o Pole podstawy graniastosłupa. Skoro graniastosłup prawidłowy czworokątny to P = x² , czyli:

	a√2		a√2		2a2		a2
Pp =		*		=		=
	2		2		4		2

2^o Teraz tylko trudniejszy moment − czyli obliczenie wysokości graniastosłupa: Plan jest taki, aby obliczyć przekątną ściany bocznej bo potem już pójdzie z tw. Pitagorasa. Teraz tylko korzystam z definicji funkcji trygonometrycznych: − rozpatruje trójkąt prostokątny, który przy ∡D ma kąt α. (połowa przekątnej; oznaczę sobie przekątną ściany bocznej jako d)

	a   2
cosα =		/ * d
	d

	a
dcosα =		/ : cosα
	2

	a   2		a
d =		=
	cosα		2cosα

Tak jak pisałem teraz z twierdzenia Pitagorasa: H² + x² = d²

	a√2		a
H2 + (		)2 = (		)2
	2		2cosα

	a2		2a2
H2 =		−
	4cos2α		4

	a2 − 2a2cos2
H2 =
	4cos2α

	a2(1 − 2cos2α)
H2 =
	4cos2α

	a2(1 − 2*(1 − sin2α))
H2 =
	4cos2α

	a2(1 − 2 + 2sin2α
H2 =
	4cos2α

	a		2sin2α − 1
H =		* √
	2		2cos2α

	a
H =		* √tg2α − 1
	2

3^o Podstawiając do wzoru: V = P_p * H

	a2		a
V =		*		* √tg2α − 1
	2		2

	a3 * √tg2α − 1
V =
	4

	a√2
Masz swoją odpowiedź , natomiast dero2005 pomylił się w		bo zapomniał napisać
	2

	2a2
dwójki w
	4

rumpek: dero2005 takie pytanie: gdybym na maturze nie zamieniał do tg to zaliczyliby wynik? na samych sinusach i cosinusach ? Bo skąd mam wiedzieć co jest w odpowiedziach

bv: dziękuję

dero2005: nie wiem, nigdy nie pisałem matury