Oblicz
Basia: Oblicz objętość i pole całkowite graniastosłupa prawidłowego ośmiokątnego o krawędziach a.
3 gru 14:49
sushi_ gg6397228:
i w czym masz problem−−−> wzory znasz
3 gru 14:52
Basia: problem z obliczeniem podstawy
3 gru 15:02
sushi_ gg6397228:
osmiokat foremny==8 trojkatow rownobocznych o boku a
3 gru 15:03
Basia: te trójkąty są przecież równoramienne, a nie równoboczne i dlatego mam problem. To jest
ośmiokąt, a nie jakiś sześciokąt, co ma trójkąty równoboczne. Narysuj sobie ośmiokąt i
sześciokąt i zobacz
3 gru 15:06
sushi_ gg6397228:
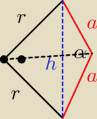
h=r*
√2 −−> h
2= 2r
2
mamy8kat−−> wiec kazdy kat ma 135stopni, zatem α=135
o
tw cosinusow
h
2=a
2+a
2−2*a*a*cos α
2r
2=a
2+a
2−2*a*a*cos 135
o −−>r
2=....
| | r*r* sin 45o | |
Podstawa to 8 trojkatow kazde pole to = |
| |
| | 2 | |
3 gru 15:26
dero2005:
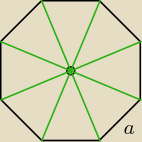
P
p = 2a
2(1 +
√2)
3 gru 15:29
Eta:
P(ośmiokąta foremnego boku "a")=
2a2(1+√2)
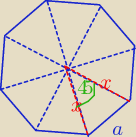
wykazuję:
360
o: 8= 45
o
| | 1 | |
PΔ= |
| x*x*sin45o => P(ośmiokąta) = 2*x2√2 |
| | 2 | |
z tw. cosinusów a
2= x
2+x
2−2x*x*cos45
o = 2x
2−x
2√2
| | a2 | | a2(2+√2) | |
to: x2= |
| = |
| |
| | 2−√2 | | 2 | |
| | a2(2+√2) | |
P=2* |
| *√2= a2(2√2+2)= 2a2(1+√2) |
| | 2 | |
P(ośmiokąta)=
2a2(1+√2)
3 gru 15:30
Basia: Dziękuję bardzo za pomoc
3 gru 15:31
Eta:
3 gru 15:34