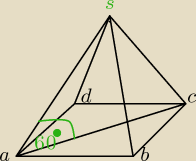
Zadanie klich: Rysunek przedstawia ostroslup prawidlowy czworokatny. pole trojkota ACS jest rowne 12√3 a)oblicz pole powierzchni całkowitej tego ostroslupa b)wyznacz cosinus kata nachylenia sciany bocznej do podstawy Bardzo prosze o pomoc niestety tego nie rozwiaze bo nie umiem

dero2005:

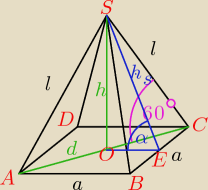
d
	*h = 12√3 → z warunków zadania
2

h
	= tg 60o = √3 → z trójkąta OCS
d   2

d		h
	=
2		√3

wstawiamy do pierwszego

h
	*h = 12√3 |* √3
√3

h² = 12*3 = 36 h = √36 = 6 z trzeciego wzoru

	2h
d =		= 4√3
	√3

	d√2
a =		= 2√6 → z trójkąta ABC (Pitagoras)
	2

h_s = √h² + (^a₂)² = √36 + 6 = √42 → z trójkąta EOS (Pitagoras) P_c = a² + 2a*h_s = 24 + 2*2√6*√42 = 24 + 24√7 = 24(1 + √7)

	h		6		1
sin α =		=		=		√42
	hs		√42		7

klich: Dziekuje Ci Bardzo

ada: Cosinus trzeba wyliczyc nie sinus