Szkicowanie wykresów funkcji.
tomek: Naszkicuj wykres dowolnej funkcji, której zbiór wartości jest równy:
(−2;2) U (2;nieskonczonosci) − wiem, ze moga byc rozne rysunki, ale chce zobaczyc, czy mam ok
mniejwiecej.
i teraz drugie zadanko
Naszkicuj wykres funkcji f: <−2;6> > R, której zbiór wartości jest równy
<−2;6) − tutaj też narysowałem, ale nie jestem pewien i chcę to sprawdzić
2 gru 15:27
sushi_ gg6397228:
to narysuj swoje rysunki, to zobaczymy czy jest OK
2 gru 15:41
tomek:
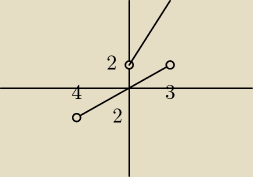
tutaj jest pierwszy rysunek
po lewej stronie jest −4, a na dole −2, nie wchodził coś znak minus. Jest dobrze?
2 gru 16:03
tomek:
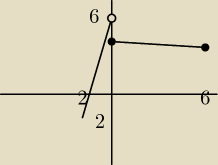
a tutaj już drugi rysunek
po lewej stronie −2 i na dole −2 , moim zdaniem zachodzi każda zależność : D
może tak być?
2 gru 16:06
sushi_ gg6397228:
a nie mozna bylo zrobic paraboli w zadaniu 2 tylko tak kombinowac//
wszystko jest OK
2 gru 16:13
tomek: jestem na kierunku mat−fiz i jeszcze nie mialem funkcji kwadratowej, matematyczka moja
powiedziala, ze mozna, ale póki co zaleca takie rysunki. Dziękuję za odpowiedź
Pozdrawiam.
2 gru 16:15
krystek: rys z godz 16:003 nie jest wykresem funkcji.
2 gru 16:22
tomek: dlaczego? to jak to trzeba zrobić?
2 gru 18:07
krystek: nie mogą leżeć "nad sobą" bo dla x∊(0.3) masz po dwie wartości ,a to nie jest funkcja.
2 gru 18:11
sushi_ gg6397228:
bo nie zauwazylem, ale dla jednego "x" sa dwa "y'
2 gru 18:11
tomek: to dwa rysunki są złe?
2 gru 18:13
sushi_ gg6397228:
tak nie moga byc kreski, bo kolor zielony sie pokrywa
2 gru 18:15
tomek: to narysujcie mi poprawny wykres, bo już sam nie wiem
2 gru 18:17
krystek: Dla pierwszej funkcji.Przesuń w prawo ,aby nie leżały jedna nad drugą.
2 gru 18:17
sushi_ gg6397228:
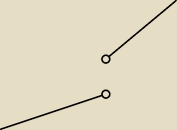
tak moze byc, tylko musisz teraz dopasowac to do swoich zalozen
nigdzie kreski nie nie pokrywaja
2 gru 18:18
tomek:
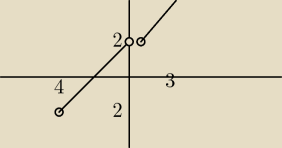
Teraz wykres 1 dobrze?
2 gru 18:20
krystek: Jeżeli dziedzina są wszystkie liczby rzeczywiste ,to prawe puste kółko musi nakładac sie (masz
lukę )
2 gru 18:23
tomek: ale to jest dowolnej funkcji, więc tak też może chyba być?
2 gru 18:25
krystek: tak! jeżeli nic nie ma w zadaniu o dziedzinie.
2 gru 18:25
tomek: okej, a teraz jak są liczby rzecziwiste, to wystarczy, że te kółeczko podepne do 2? wtedy nie
wyjdzie zależność (−2;2) U (2; nieskonczosci) tylko wyjdzie (−2; nieskonczonosci) . no jak?
2 gru 18:27
tomek: i jeszcze mam jedno pytanie. skoro 2 przyklad jest dobrze wykonany (bo mowicie ze ok) to dla
mnie teraz jest dziwnie, bo dla argumentu 0 przyjmuje wartosc prawie 6 i jakas tam liczbe
calkowita np. 5. no dziwne, dziwne , wyjasnijcie mi to. jak mozecie
2 gru 18:44
Basia:
nie przyjmuje wartości 6; przecież masz tam kółko niezamalowane
2 gru 18:47
tomek: No tak, dlatego mówię, że nie całe 6, czyli jak jest otwarty i zamknięty przy tym samym
argumencie jak w przkładzie moim to tak może być? Czyli jest okej rysunek?
2 gru 18:49
krystek: dla x=o "lewa " funkcja nie przyjmuje wartości 6 a druga funkcja przyjmuje np wartość 5.
Gdyby w 6 było zamalowane kółko wówczas nie byłby to wykres funkcji, ponieważ dla x=0 miałbyś
wartośc y=6 i y=5.
Myślę ,że już rozumiesz.
2 gru 18:54
krystek: Tak ok!
2 gru 18:55
tomek: Tak, już wszystko rozumiem, zapomniałem kompletnie o tym, że jak dla jednego argumenty
przyjmujemy dwa argumenty to nie jest to funkcja.
2 gru 18:57
krystek: Pozwól,że poprawie −"dla jednego argumentu dwie wartości"
2 gru 19:02