:( ICSP: Kąt B trójkąta ABC jest równy 60^o. Dwusieczne AD i CE przecinają się w punkcie M.Udowodnij że |MD| = |ME|. Jakaś podpowiedź?

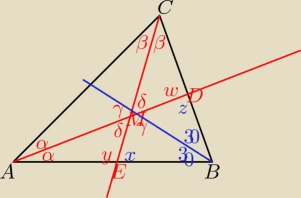
Basia: 2α+2β+60 = 180 2(α+β) = 120 α+β=60 ⇒ γ=120 ⇒ δ=60 y = 180 − α − 60 = 120 −α x = 180 − (120−α) = 60+α w = 180 − β − 60 = 120 − β z = 60+β = 60+(60−α) = 120−α

sinx		sin30		1
	=		=
BM		ME		2ME

sinz		sin30		1
	=		=
BM		MD		2MD

BM = 2ME*sinx BM = 2MD*sinz sinx = sin(60+α) = sin60*cosα+ sinα*cos60 sinz = sin(120−α) = sin120*cosα − sinα*cos120 dalej licz sam (już widać)

ICSP: sin60^o = sin120^o cos60^o = −cos120^o czyli minus w sinz zmienia się na + i powstanie równość Dziękuję bardzo

Basia: może dałoby się coś bardziej eleganckiego wymyślić, ale z kątów to tak szybko wychodzi ....

ICSP: a można od razu ze wzórów redukcyjnych sin(120 − α) = sin(180 − (120 − a) = sin(60 + a)

Eta: ICSP Mam prostszy sposób na to zadanie

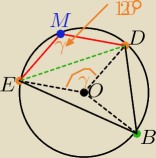
Eta: Wskazówka: |∡EMD|=γ= 120^o |∡B|= 60^o to: γ+B= 180^o wniosek na czworokącie MEBD da się opisać okrąg teraz dokończ .... to już "pikuś"