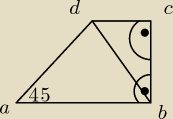
Trapezy Karolina: Pomocy! Trapez ABCD jest prostokątny. Na podstawie danych na rysunku poniżej oblicz długość dłuższej podstawy AB. bd=5 ad=4√2

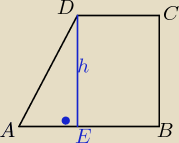
lula: obliczam |AE| cos45'=|AE|/4√2 ^√2₂=|AE|/4√2 |AE|=4 obliczam h czyli |DE|=|BC|

	h
sin 45'=
	4√2

√2		h
	=
2		4√2

2h=8 h=4 z tw. PIT. |DC|²+|BC|²=|DB|² |DC|²=5²−4²=9 dc=3 a że DC|=|EB| to |AB|=|AE|+|EB|=4+3=7

Karolina: faktycznie nie pomyslalam ze mozna tu poprowadzic wysokosc... teraz juz wiem dziekuje mam jeszcze problem z dwoma trapezami, moglabyc mi pomoc?

aa: dawaj

Karolina:

aa: i co

Karolina:

aa: ale co trzeba liczyć?

Karolina: nalezy policzyc dlugosc dluzszej podstawy ab

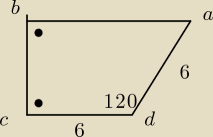
aa: suma kątów w czworokącie jest równa 360' więc kąt a =360−(120+90+90)=60' z D prowadzisz wysokość do punktu E i masz nowy trójkąt prostokątny DAE

	|AE|
cos60'=
	|DA|

1/2=|AE|/6 |AE|=3 |AB|=|AE|+|EB| gdzie |EB|=|CD|

aa: a w tym ostatnim co trzeba?

Karolina: tez to samo

Karolina: i jeszcze jedno prosze W okrag o srodku O wpisano czworokat abcd. Wyznacz miary katow tego czworokata oraz miare kata ostrego utworzonego przez jego przekatne, jesli: a)K AOB=120, K BOC=120 i K COD=40 b)K AOB=150, K AOD=60 i K COD=70

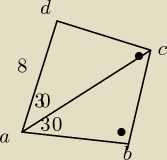
aa: kąt ABC=90' kat CAB=30' więc kąt BCA=60' a ze kąt BCD jest prosty to kąt ACD=90'−60'=30' jeśli kąt DAC=30' i kąt ACD=30' to trójkąt ACD jest równoramienny więc |AD|=|DC|=8 i znów wysokość z punktu D do E cos60'=|AE|/|AD| 1/2=|AE|/8 |AE|=4 i znów |AB|=|AE|+|EB| a |EB|=|DC|=8

Karolina: dziekuje a to co dodalam zrobilbys/abys?

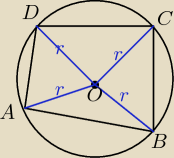
aa: to są trójkąty równoramienne więc

	180−120
jeżeli kąt AOB=120' to kat OAB=ABO=		itd a potem tylko pododawać odpowiednie kąty
	2

Karolina: ok dzieki