Wyznaczyć
alfa: Wyznacz punkty przegięcia oraz przedziały wklęsłości i wypukłości funkcji.
h(x)=x
2*lx, x>0
Liczę pierwszą pochodną i otrzymuje h'(x)=(x
2 *lnx)'=(x
2)'*lnx+x
2(lnx)'=2x* lnx+x
2
Liczę drugą pochodną i otrzymuje h''(x)=x(2lnx+1)=(x)'(2lnx+1)+(x)(2lnx+1)'=2lnx+3
h''(x)=0 ⇔ 2lnx+3=0
2lnx+3=0
x=e
−3/2
1 gru 16:44
alfa: I teraz pytanie jak stwierdzić kiedy funkcja jest wklęsła czy wypukła?
1 gru 16:46
alfa: Ma ktoś pojęcie jak sprawdza się zmianę znaku w takich przypadkach z e?
1 gru 17:03
Ed: e to zwykla liczba

1 gru 17:06
alfa: No tak, tylko jak sprawdzić czy jest zmiana z "−" na "+", lub odwrotnie. Bo nie czaję tego za
bardzo.
1 gru 17:09
Ed:
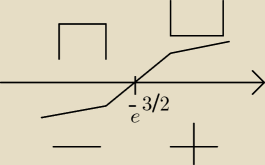
1 gru 17:11
alfa: W przypadku e3/2 jest identyczny wykres. Jak to się ustala?
1 gru 17:14
Ed: rysujesz tak jak w nierownosciach wielomianowych od prawej strony, gora czy dol to zalezy od
znaku przy najwyzszej potedze x a to czy odbijasz wykres czy przechodzisz przez os zalezy od
krotnosci tych rozwiazan dla f''(x)=0
1 gru 17:24
alfa: To akurat wiem i nie mam z tym problemu. Czyli reasumując dla x∊(0,e{−3/2} f''(x)<0, więc
funkcja jest wklęsła w tym przedziale. Dla x∊(e{−3/2},
∞) f''(x)>0, więc funkcja jest wypukła w
tym przedziale.
| | 3 | | 3 | |
Punkt przegięcia to (e−3/2,− |
| e−3) Tylko nie wiem czy ta wartość − |
| e−3 jest |
| | 2 | | 2 | |
okej, po wstawieniu do x
2 * lnx.
1 gru 17:44

