funkcja wymierna - rysowanie i parametr ola:

	|x2 − 1|
funkcja f dana jest wzorem f(x) =		.
	x3 −x

a. naszkicuj wykres funkcji f b. dla jakich wartości parametru m równanie ma jedno rozwiązanie? Błagam o pomoc, kompletnie nie wiem jak sie do tego zabrać. Wiem, że trzeba rozpatrzeć dwa przypadki, w zależności od wartości bezwzględnej. Ale co dalej?

Jack: wsk. zauważ, że x³−x=x(x²−1) i zerknij na licznik.

tedua: W sumie to będą 3 przypadki |x²−1|=|x−1| |x+1| mianownik można rozpisać jako x(x²−1)=x(x−1)(x+1) więc dziedziną będą liczby R\{−1,0,1} ¹_x dla x<−1 f(x) = −¹_x dla −1<x<1 ¹_x dla x>1 Wykresem będzie funkcja homograficzna odpowiednio w przedziale 1 i 3. a w tym 2 −1<x<1 odwrotna. Z wykresu odczytasz parametr m.

ola:

	1
no tak, wychodzi mi, że dla x ∊ (−∞, −1)∪(1, +∞) wychodzi		, dla x∊(−1,1) bedzie
	x

	1
−		. tylko jak narysowac ten drugi przedział,. skoro D=R−{−1, 0, 1} go jakby wyklucza?
	x

tedua: no tak więc przy x=1 kółko będzie otwarte tak jak i przy x=−1. a do 0, czyli OY wykres też nigdy nie dochodzi.

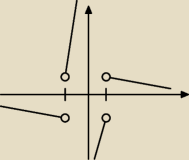
tedua: przepraszam za jakość ale powiedzmy że coś takiego. oczywiście to nie są proste.

ola: ooo dzieki piekne, teraz juz mam wyobrazenie jak to ma wygladac