:) hmm... majka: w ostrosłupie prawidłowym sześciokątnym cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy wynosi 0,2. Wysokość ostrosłupa ma długość 4√3. Oblicz objętość tego ostrosłupa. Próbowałam to rozwiązywać sama ale nie wyszedł mi wynik zgodny z odpowiedzią, pomagał mi też ktoś na forum ale jemu tez wynik wyszedł inny. Proszę o pomoc Odpowiedz do zadania to V = 12 https://matematykaszkolna.pl/forum/114288.html

stah: zadanie z linku jest dobrze rozwiazanie ( no prawie) ubytek w wzorze V=1/3*Pp*H V=1/3*3√3*4√3=36*1/3=12

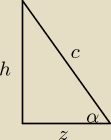
stah: h=4√3 1.ostroslup ten ma w podstawie szescikat, a wiec 6 trojkatow rownobocznych wzór na pole podstawy to ^6z2√3₄ Dazymy do wyznaczenia z 2..cosα=0,2 → Obliczam sinusa z jedynki trygonometrycznej cos²α + sin^α=1 → ⁴₁₀₀ + sin²α=1 sinα=^√96₁₀₀ = ^4√6₁₀ 3..Szukam boku C sinα=^h_c → ^4√6₁₀=^4√3_c − mnozysz na krzyz 4√6c=40√3 √6c=10√3 c=^10√3₆ − usuwasz niewymiernosc c=5√2 4. Z z funkcji trygonometrycznych cos²₁₀=^z_5√2 10z=10√2 z=√2 a wiec teraz z podstawiamy do wzoru z pkt 1. Pp = ^6*2√3₄ = 3√3 V=1/3*Pp*h