OPERON, matura próbna Hiromi_Ise: Wierzchołki trójkąta równobocznego ABC leżą na paraboli, bedącej wykresem funkcji f(x) = x² − 6x. Punkt C leży w wierzchołku paraboli. Znajdź współrzedne jednego z pozostałych wierzchołków trójkąta. I tak: wyliczyłam, że wierzchołek jest w punkcie C=(3, −9) i nie mam pojecia jak to dalej robić, ktoś pomoże?

Hiromi_Ise: up

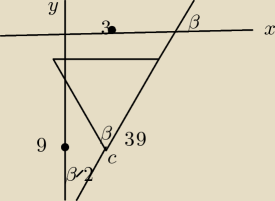
+-: na rysunku oś y powinna być bardziej na lewo 9 to jest −9 β=60 Trójkąt równoboczny. Równanie prostej y=xtg60+b b=−9 − 3√3 czyli y=x√3 −9−3√3 x√2−6x=x√3 −9−3√3 x₁=3 ;x₂=3+√3 postawiając x₂ pod y=x√2−6x otrzymujemy y=−6 jest to równanie prostej na której leży bok równoległy do osi x , a więc i wsółrzędne y wierzchołów A i B

Ratarcia: skąd się wzięło x√2 −6x= x√3 itd...

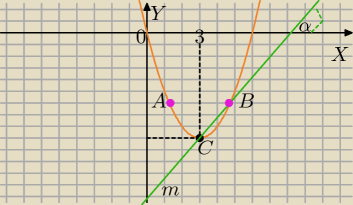
Mila: α=60⁰ m: y = √3x−9−3√3 Kiedy wykresy się przetną? x²−6x=√3x−9−3√3 porównanie x²+x(−6−√3)+9+3√3=0 Δ=3 √Δ=√3 x₁=3+√3 lub x₂=3 wsp. wierzchołka y₁=√3*(3+√3)−9−3√3=−6 B(3−√3;−6) A(x,−6) oblicz

tyszcz: Przepraszam za odkopanie ale mam pytanie czy tutaj wierzchołki A i B nie mogą leżeć tam gdzie miejsca zerowe ?

tyszcz: Przepraszam nie doczytałem.. Tak by mogło być gdyby trójkąt był równoramienny a nie równoboczny.