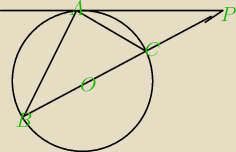
geometria Julia: Dany jest okrąg o środku O. Z punktu P poprowadzono styczną do okręgu w punkcie A oraz sieczną przecinającą okrąg w punktach B, C i przechodzącą przez środek okręgu.(rysunek obok). Odległość punktu C od prostej AP jest równa , a odcinek CP ma długość 3. Oblicz promień okręgu i pole trójkąta ABC. Domyślam się, że trzeba coś policzyć z Pitagorasa i Talesa, ale nie wiem, jak to ugryśc :\

Patryk: kat bac masz 90⁰ jest oparty na srednicy

Julia: i co mogę z tym zrobić?

Patryk: sam jeszcze nad tym myślę

Patryk:

	3
prostej AP jest równa		, nie zapomniałaś przepisać ?
	2

Julia: faktycznie, zapomniałam

Julia: ma ktoś jakiś pomysł?

Kasia: |OC|=|CP| , czyli juz masz promień równy 3. AP z Pitagorasa . 3²=(3/2)²+ x² I wynik razu 2 i masz AP. A pole trójkąta to tak : podstawa to średnica , masz promień czyli średnicę też . I nie wiem jak znaleźć wysokość.. może trzeba tam trójkąta prostokątnego zrobić o najdłuższej ścianie równej |CA| czyli 3 , o jednej przyrostokatnej równej połowie promienia .. Ja coś takiego robiłam , ale to tylko moje podejrzenia .