rozwiazanie przykladu walu: potrzebuje pomocy: jak rozwiazac podany przyklad 2sin²x−cosx−1<0

Basia: 2(1−cos²x) − cosx − 1 < 0 2 − 2cos²x − cosx −1 <0 −2cos²x − cosx +1 < 0 t = cosx −1 ≤ t ≤ 1 −2t² − t + 1 <0 rozwiązujesz najpierw tę nierówność kwadratową potem dopiero wracasz do cosinusa

Bizon: 2(1−cos²x)−cosx−1<0 −2cos²x−cosx+1<0 podstawiaj .... i walcz−

rumpek: sin²x = 1 − cos²x 2(1 − cos²x) − cosx − 1 < 0 2 − 2cos²x − cosx − 1 < 0 −2cos²x − cosx + 1 < 0 t = cosx, t∊<−1;1> −2t² − t + 1 < 0 Δ = 1 + 8 = 9 ⇒ √Δ = 3

	1 − 3		−2		1
t1 =		=		=
	−4		−4		2

	1 + 3		4
t2 =		=		= −1
	−4		−4

	1
(t −		)(t + 1) < 0
	2

	1
t>−1 ⋀ t <
	2

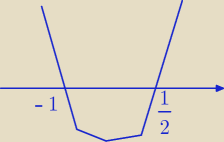
Czyli:

	1
cosx > −1 ⋀ cosx <
	2

I rysujesz na cosinusoidzie połączone warunki

walu: tak i z rownania kwadratowego wychodzi t1= −1 lub t2= 1/2 i co dalej ? nie rozumiem tego: −1 <t <1

walu: ok dzieki za pomoc juz rozumiem

walu: t>−1 ⋀ t <1/2 dlaczego t >−1 i t<1/2 ?

rumpek: Stfu zaraz od nowa parabola zła

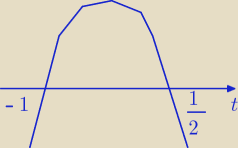
rumpek: mamy:

	1
−(t + 1)(t −		) < 0
	2

czyli w tym wypadku będzie

	1
t < − 1 ⋁ t >
	2

rumpek: Jak można "minus" z "plusem" pomylić tylko mi to się zdarza xD

walu: a jak bedzie to wygladac na wykresie ?

rumpek: Przecież nie narysuje tu cosinusoidy

walu: czyli wg mnie musimy odrzucic t <−1 wiec zostaje t>1/2 wiec rozwiazanie to −pi / 3 do pi/3 +2kpi?

Basia: nie tylko Tobie rumpek