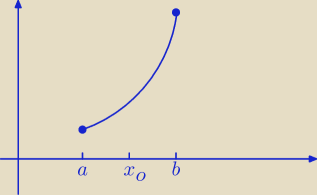
Ciągłość Godzio: Witam, mam udowodnić, że funkcja wypukła jest ciągła, Spełnia ona nierówność f((1 − λ)a + λb) ≤ (1 − λ)f(a) + λf(b) Pokażę tylko skrawek rozwiązania, bo nie wiem czy poprawnie to oszacowałem. (1 − λ)a + λb = x wtedy nierówność przyjmuje postać:

	b − x		x − a
f(x) ≤		f(a) +		f(b)
	b − a		b − a

Mam pokazać: ∀ε>0 ∃δ>0 ∀x (|x − x₀| < δ ⇒ |f(x) − f(x₀)| < ε ) |f(x) − f(x₀)| ≤ [ po szacowaniu ]

	|f(a)| − |f(b)|		|f(b)| − |f(a)|
2|f(a)| + (x − x0) *		+ 2x0 *		<
	b − a		b − a

	|f(a)| − |f(b)|		|f(b)| − |f(a)|
2|f(a)| − δ *		+ 2x0 *		= ε
	b − a		b − a

Godzio: odświeżam

Basia: nie bardzo wiem jak to szacowałeś liczyłeś f(x) − f(x₀) na mocy tej pierwszej wyprowadzonej nierówności ?

	x0−x		x−x0
f(x) − f(x0) ≤		*f(a) +		*f(b) =
	b−a		b−a

x−x0
	*[f(b) − f(a)]
b−a

i co dalej ? bo nie wiem

Basia: o ile dobrze kojarzę to tu trzeba wykorzystać tw. o wartości średniej pamiętając, że skoro wypukła to f"(x) > 0 ⇒ f'(x) stale rosnąca

Godzio: Nie mogę korzystać z pochodnych Ogólnie wykorzystując pare rzeczy do tego doszedłem, ale chyba nie tak jak Ty to zapisałaś bo ja mam przedział a,b gdzie x i x₀ do niego należą

Basia: a nie masz rację, pomyliłam się ale nadal nie wiem jak to szacowałeś |f(x)| −|f(x₀)| ≤ ||f(x) − f(x₀)| ≤ |f(x)|+|f(x₀)| z tego korzystałeś czy z czegoś innego ?

Godzio: Tak, z tego, a później z nierówności wynikającej z wypukłości i doprowadziłem do takiej postaci jak zapisałem

Basia: no to jeżeli nie pomyliłeś się w rachunkach to jest dobrze

Godzio: Sprawdzałem kilka razy jestem z siebie dumny a jeszcze jedno, teraz pisze że całość = ε i to koniec, czy mam wyznaczyć z całości δ ?

Basia: masz wyznaczyć δ i napisać ∀_ε>0∃_{δ= tyle i tyle} ......... na ale to już pikuś

Godzio: Ok, dzięki za pomoc