Pole koła, pole trójkąta Geoetria płaska: W trójkącie równoramiennym ABC podstawa AB ma długość 26 cm. Długość wysokości AE jest równa 24 cm. Oblicz obwód trójkąta ABC. Wytłumaczy mi to ktoś krok po kroku? Bardzo proszę

imralav: A znasz wynik? Coś tu policzyłem, ale nie wiem czy się zgadza, czuję, że to powinny ładnie całkowite wartości wychodzić, a nie z rozwinięciami po przecinku ; p

Geoetria płaska: Obw=93,6cm

imralav: No u mnie obwód to 88,34. Coś musiałem po drodze namieszać.

Geoetria płaska: Nie martw się, ja też sporo namieszałam i wydaje mi się, że są złe odpowiedzi w książce .... A wrzuć rozwiązanie, ok?

sushi_ gg6397228: zauwaz, ze masz wysokosc nie z wierzcholka (tam gdzie ida ramiona) tylko z podstawy

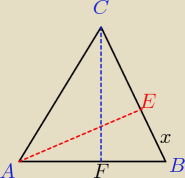
imralav: Poprawka, 88,4, nie potrzebnie jakoś na około szedłem. Pokażę jak ja to rozumiem: X można wyliczyć z twierdzenia pitagorasa, x = √26²−24² = 10 trójkąty ABE i FBC są podobne (te same kąty) więc można wyliczyć ^x_|FB| = ^|AE|_|CF|, stąd |CF| = ^|FB|*|AE|_x = 28,8, potem z pitagorasa liczymy bok trójkąta |CB| (po wyliczeniu 31,2). Sumując długość podstawy i boków otrzymujemy 88,4

Geoetria płaska: Wiem, wys. poprowadziłam z wierzchołka A, który jest przy podstawie pod kątem prostym do ramienia CB ...

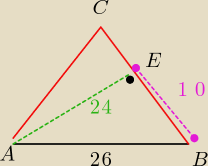
sushi_ gg6397228: I Pitagorasa kolor różowy==10 potem Pitagoras dla trojkata AEC −−> boki 24, x, (10+x)

Geoetria płaska: Dokładnie tak samo robiłam i mi ciągle inne wyniki wychodzą ... Może mam złą proporcje. Moment, spróbuję jeszcze raz ...

Geoetria płaska: Kurcze, za szybko piszecie i moje odpowiedzi są do tyłu

imralav: Czyli tak skorzystać z podobieństwa jak ja to zrobiłem nie można?

imralav: wg tego, co napisał Sushi wychodzi tak jak w książce.

imralav: Aż mi wstyd, że sam o tym nie pomyślałem ; x

Geoetria płaska: No tak, ale nie rozumiem jednej rzeczy .... Bo to bym chyba miało wyglądać tak: 24²+(x+10)²=x² 576+x²+20x+100=x² 20x+676=0 (x² się zredukowało) 20x=−676 /:20 x=−33,8 Wszystko byłoby ok, gdyby nie to, że x wychodzi ujemny ... Dlaczego? Gdzie się pomyliłam?

imralav: 24² + x² = (10+x)²! Przeciwprostokątną jest 10+x ; )

imralav: W podobny sposób się pomyliłem na maturze próbnej w zeszłym tygodniu, tyle z moich stu procent ; x

Geoetria płaska: Oj biedaku, ale nie przejmuj się, to była dopiero próbna Dzięki wielkie za pomoc

imralav: Już nawet nie chodzi o wynik ale o to, że w głupi sposób tracę punkty. Nie ma za co, miłego dnia ; )

Geoetria płaska: Aha, mam jeszcze jedno pytanie. Bo na rysunku jest dwa razy zastosowane x. Czy tu nie występuje kolizja oznaczeń?

imralav: Jeśli masz na myśli mój rysunek − pooznaczany był pod liczenie proporcjami, stąd ta kolizja. Po prostu wystarczyłoby tam zamiast x wpisać 10, a dopiero pozostałą resztę odcinka |AB| oznaczyć jako x, by pasowało do podanych wyżej obliczeń.