Równania i nierówności kwadratowe
Marta:
1. Dla jakiej wartości a równanie ax2+x+a=0 ma jedno rozwiązanie?
2. Zaznacz na osi liczbowej zbiór liczb, które spełniają nierówność:x2−4x−21≥0 i jednocześnie
nierówność x(x+5)>0
3. Jakie liczby całkowite są rozwiązaniem nierówności −12x2+5x−10≥0 ?
27 lis 10:38
Funfelek: 1. Kiedy jest to równanie liniowe, czyli a =0 lub kiedy jest to równanie kwadratowe ( a!=0) i
delta = 0
27 lis 10:42
pomagacz:
1. warunek Δ = 0
2. policzyć nierówności, narysować na osi i wyznaczyć wszystkie x−y
3. policzyć nierówność, narysować na osi i wyznaczyć TYLKO liczby całkowite
Policz i pokaż rozwiązania

27 lis 10:43
Funfelek: 3. Pomnóż stronami *2 ( żeby się łatwiej liczyło), oblicz i z przedziału który Ci wyjdzie
wybierz tylko liczby całkowite ( jeżeli wyjdą pierwiastki to musisz oszacować ich wartość)
27 lis 10:44
imralav: W pierwszym przypadku potrzebna Ci wiedza, kiedy równanie kwadratowe ma jedno rozwiązanie (Gdy
delta równa jest 0). Układasz równanie: Δ = b2 − 4ac, pod Δ podstawiasz zero a pod a, b i c
dane z podanego w zadaniu równania.
0 = 12 − 4a2
przenosisz 4a2 na lewą stronę:
4a2 = 1
dzielisz obustronnie przez 4
a2 = 14
pierwiastkujesz
a = −12 lub a = 12
odp: To równanie ma jedno miejsce zerowe tylko gdy a = −12 lub a = 12
27 lis 10:44
imralav: nah, jesteście zbyt szybcy ; p
27 lis 10:45
Aga: 1.
Dla a=0 równanie też ma jedno rozwiązanie.
27 lis 10:47
Marta:
Mógłby ktoś mi te zadanie rozwiązać?
Zaznacz na osi liczbowej zbiór liczb, które spełniają nierówność:x2−4x−21≥0 i jednocześnie
nierówność x(x+5)>0
27 lis 11:03
Marta: Mógłby ktos mi sprawdzic te zadanie?
Zaznacz na osi liczbowej zbiór liczb, które spełniają nierówność:x2−4x−21≥0 i jednocześnie
nierówność x(x+5)>0
Ja to tak rozwiązałam:
x2−4x−21≥0
x2−4x−21=0
a=1
b=−4
c=−21
Δ=b2−4ac
Δ=42−4*1*(−21)
Δ=16+84
Δ=100
√Δ=10
x1=−b−√Δ2a
x1=4−102
x1=−3
x2=−b+√Δ2a
x2=4+102
x2=7
x(x+5)>0
x(x+5)=0
x=0
x+5=0
x=−5
ale co dalej mam zrobić?
27 lis 11:14
pomagacz:
rysujesz oś i zaznaczasz wszystkie policzone x−y na niej, następnie zamalowujesz kółeczka na
odpowiednich x−ach i robisz przedziały, narysuj tutaj to dalej będziemy tłumaczyć

27 lis 11:22
Marta:

Tak to ma być?
27 lis 11:40
pomagacz:
ok, teraz musisz narysować odpowiednie parabole na odpowiednich parach punktów
27 lis 11:47
Marta: ale jak ja to mam narysować, tu tkwi problem

27 lis 11:48
pomagacz:
jeżeli a>0 to ramiona w górę, jeśli a<0 to ramiona w dół
27 lis 11:50
Marta:
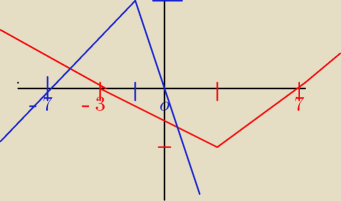
27 lis 11:55
Marta:
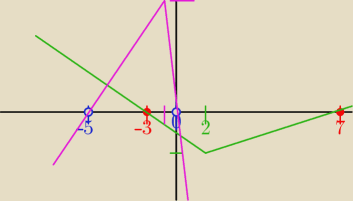
27 lis 12:09
pomagacz:

dlaczego niebieska w dół?
oba równania mają a>0
x
2 − 4x − 21 ≥ 0
x
1 = −3
x
2 = 7
x(x + 5) > 0
x
1 = 0
x
2 = −5
Większe są nad osią, mniejszew pod osią, teraz tylko odczytać i wyznaczyć te, które nachodzą na
siebie

27 lis 12:11
Marta: obliczanie wierzchołku paraboli
a) dla x1=−3
x2=7
p=−b2a
p=42
p=2
q={−Δ}{4a}
q={−10}{4}
q=−2,5
b) dla: x1=0
x2=−5
xw=x1+x22
xw=0−52
xw=−2,5
2,5=x1+x22
2,5=x1−52 /*2
5=x−5 /+5
10=x
27 lis 12:21
Marta: no ale jak sie oblicza wierzcholki paraboli?
27 lis 12:23
pomagacz:
wierzchołek:
W = (p, q)
27 lis 12:28
27 lis 12:28
Marta: no oki juz tak robilam, ale w tej drugiej funkcji nie wiem jak o sie oblicza

moglbys mi napisac jak to obliczyles?
27 lis 12:31
Tomek.Noah: ax2+x+a=0 pytanie jest kiedt to ma jedno roziwazanie a wiec w tedy kiedy a=0 bo wtedy mamy
rownanie liniowe gdzie x=0 i gdy a≠0 Δ=0 a nie jak ktos ciagle tam pisze ze tylko dla Δ=0
27 lis 13:02


 Tak to ma być?
Tak to ma być?



 dlaczego niebieska w dół?
oba równania mają a>0
x2 − 4x − 21 ≥ 0
x1 = −3
x2 = 7
x(x + 5) > 0
x1 = 0
x2 = −5
Większe są nad osią, mniejszew pod osią, teraz tylko odczytać i wyznaczyć te, które nachodzą na
siebie
dlaczego niebieska w dół?
oba równania mają a>0
x2 − 4x − 21 ≥ 0
x1 = −3
x2 = 7
x(x + 5) > 0
x1 = 0
x2 = −5
Większe są nad osią, mniejszew pod osią, teraz tylko odczytać i wyznaczyć te, które nachodzą na
siebie 
 moglbys mi napisac jak to obliczyles?
moglbys mi napisac jak to obliczyles?